Numerical Models of Axisymmetric Structures and Tanks
ELPLA (ELastic PLAte) is a software which is used for analyzing geotechnical and structure problems. One of them is analyzing axisymmetric structure or tank with the real subsoil model.
-
Three known subsoil models for the analysis of axisymmetric structures and tanks (standard models) are considered. The subsoil models are the Simple Assumption Model, the Winkler Model and the Continuum Model
-
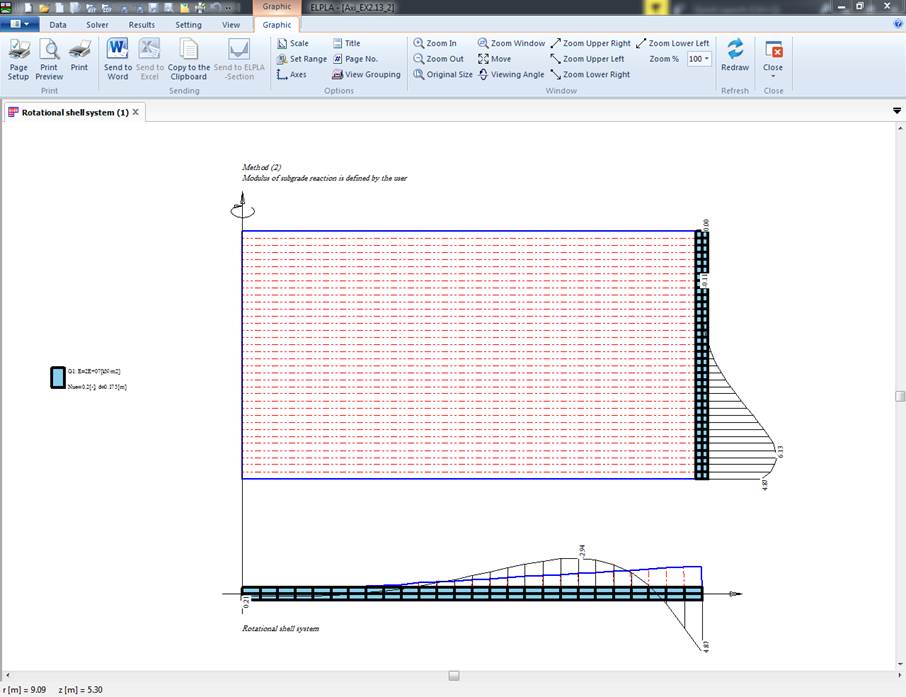
The mathematical solution of the structures is based on the FE-Method. The program can analyze different types of subsoil models, especially the Continuum model that considers any number of soil layers under the structure base
-
A good advantage of this program is the capability to handle the three analyses of flexible, elastic and rigid bases. In addition, the mesh of the rigid and flexible bases can be constructed to be analogous to the finite elements mesh of the elastic foundation. Therefore, the three analyses can be compared easily and correctly
-
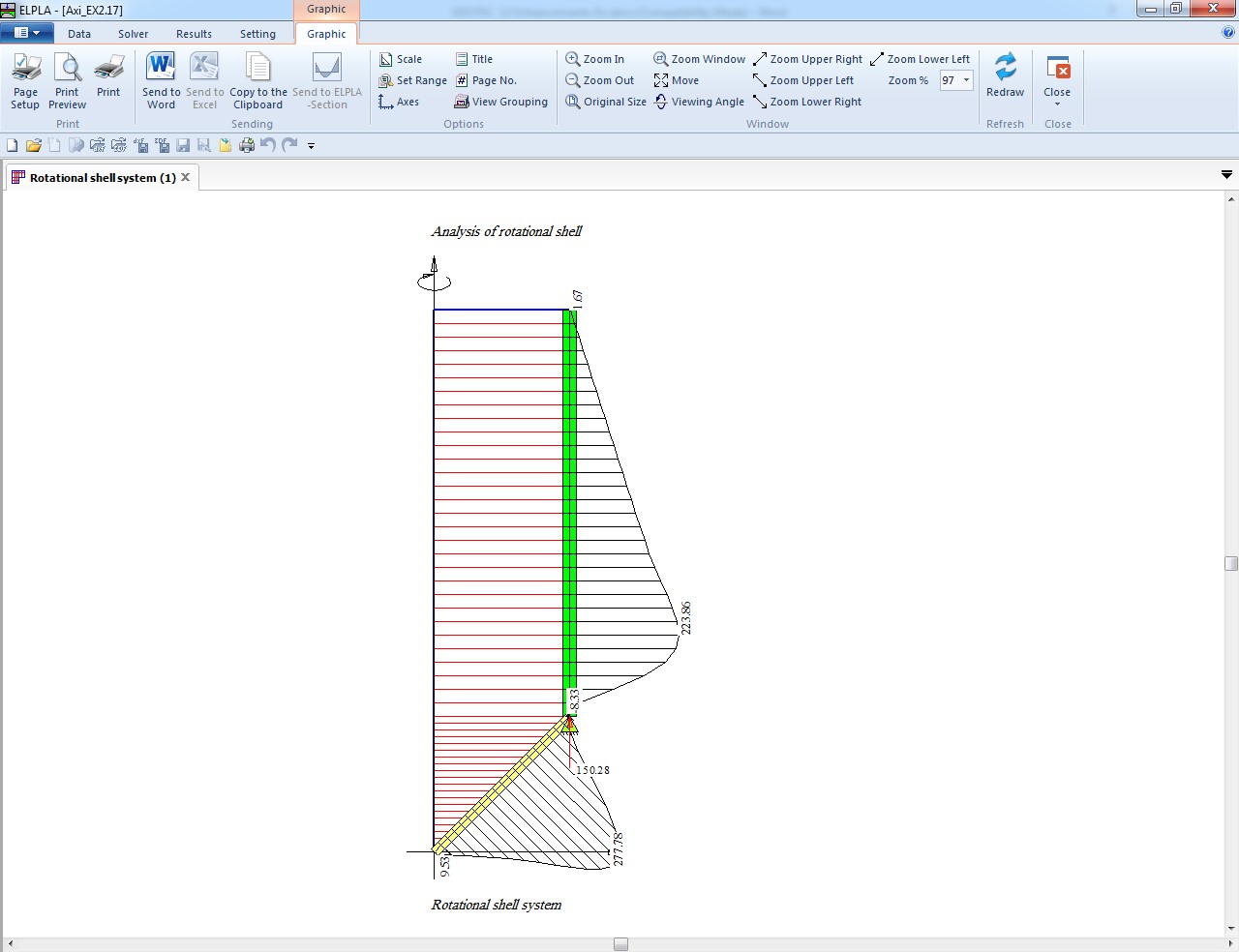
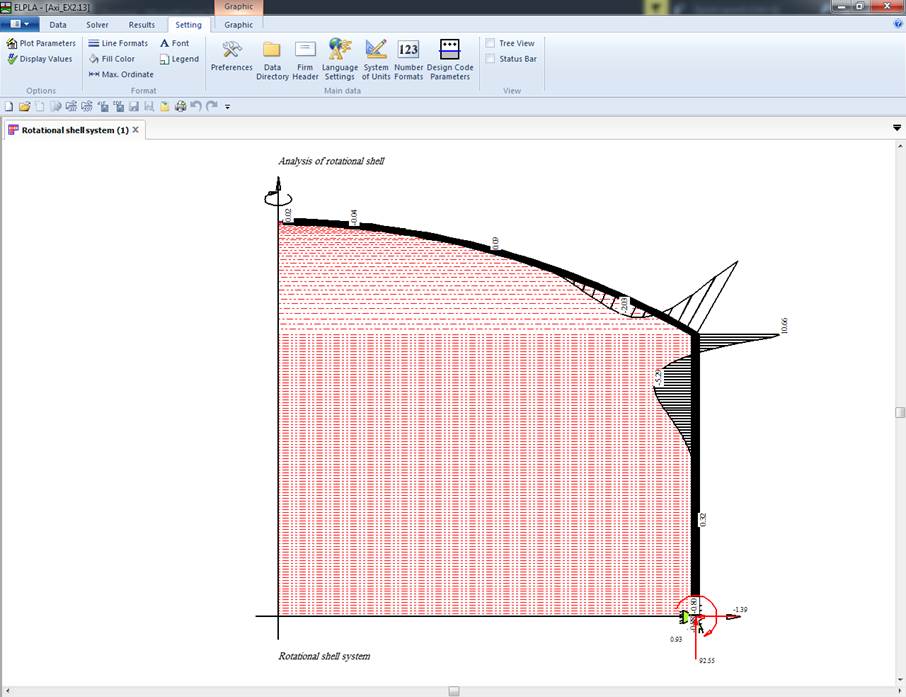
This textbook describes procedures and methods available in ELPLA to analyze circular cylindrical shells structures
-
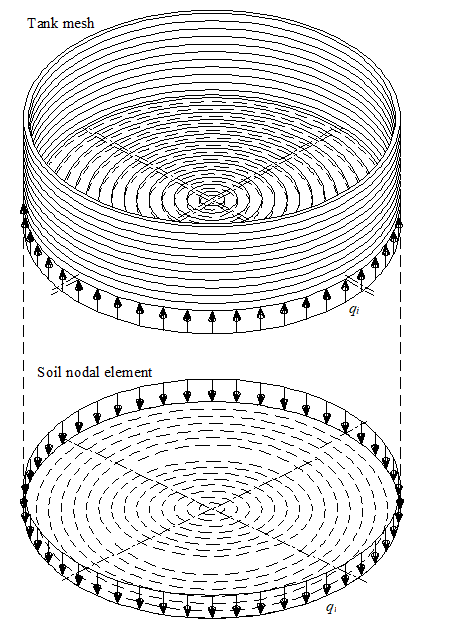
Circular cylindrical tank resting on any layered compressible soil is considered as one unit taking into account the soil-structure interaction effect
-
The purpose of this text is to present the methods, equations, procedures, and techniques used in the formulation and development of the ELPLA function for analyzing tanks on different subsoil models
-
An understanding of these concepts will be of great benefit in applying the software, resolving difficulties and judging the acceptability of the results
-
Two familiar types of subsoil models are considered, Winkler’s model and Continuum model. In addition, the simple assumption model is also considered. This model assumes linear contact pressure on the base of the tank
-
The mathematical solution of the circular cylindrical tanks is based on the Finite Element Method using axi-symmetric circular cylindrical shell elements In which, axi-symmetric shell finite elements represent the tank wall and tank base according to the nature geometry of the structure