Tiefgründungen
1- Berechnung eines axial und lateral belasteten Einzelpfahls.
2- Berechnung eines seitlich belasteten Einzelpfahles mit p-y Kurve.
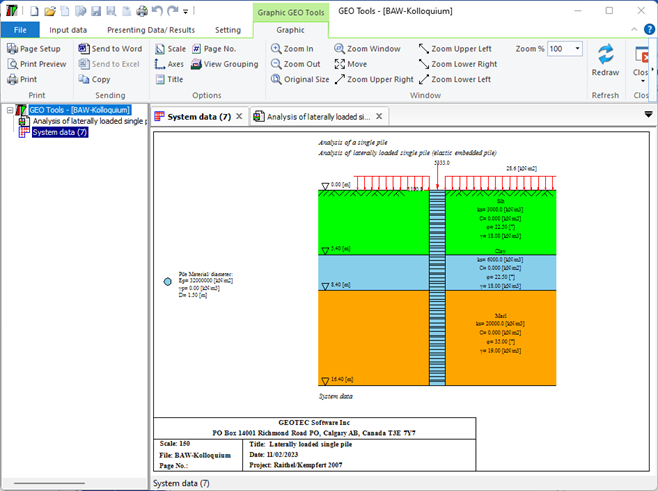
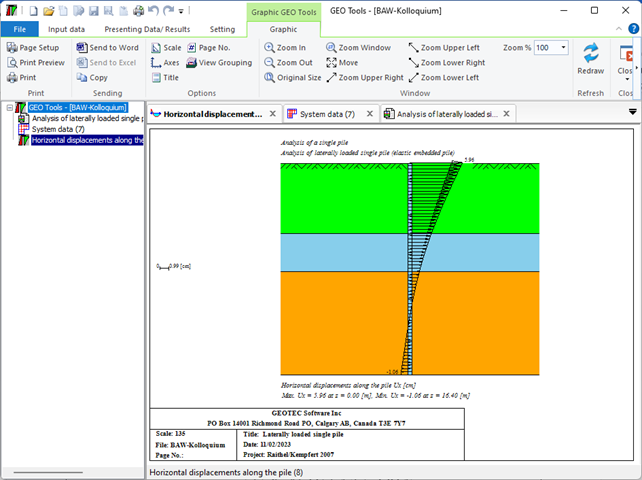
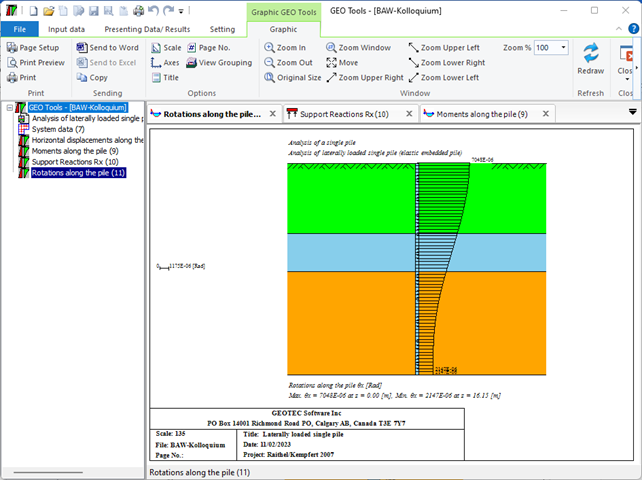
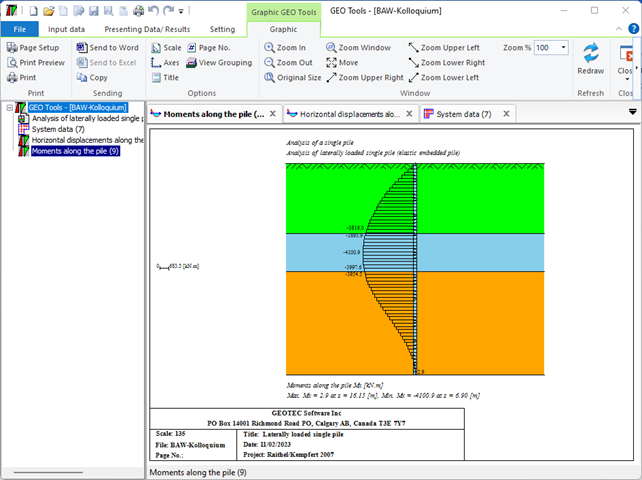
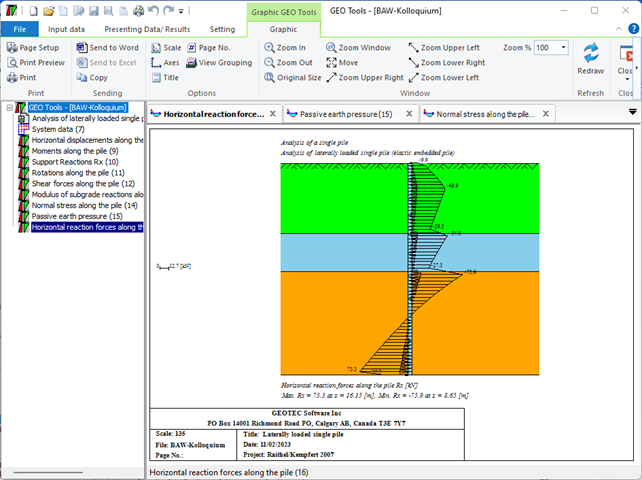
3- Berechnung eines seitlich belasteten elastischen gebeteten Einzelpfahles.
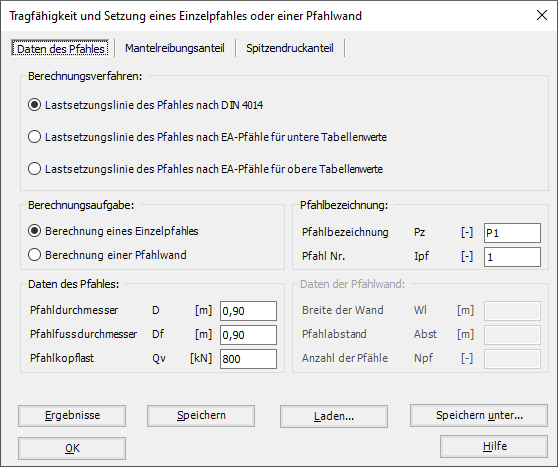
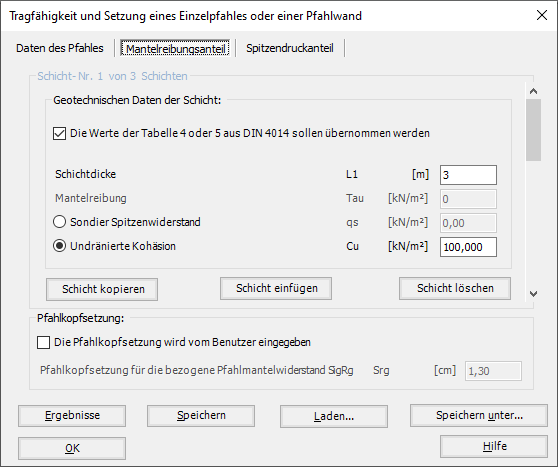
4 - Tragfähigkeit und Setzung eines Einzelpfahles oder einer Pfahlwand.
5- Berechnung einer Kombinierten Pfahl-Plattengründung.
6 - Einflusszahlen der Spannungen nach GEDDES.
7 - Spundwand.
8 - Berechnung einer Einzelbarrette.
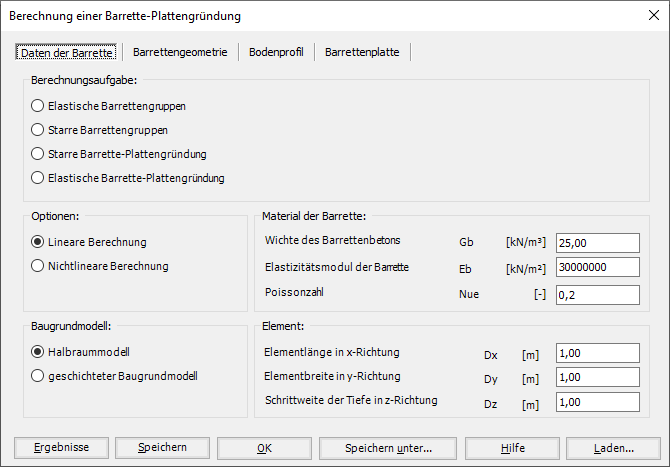
9 - Berechnung einer Barrette-Plattengründung.
10- Berechnung von Erddruck.
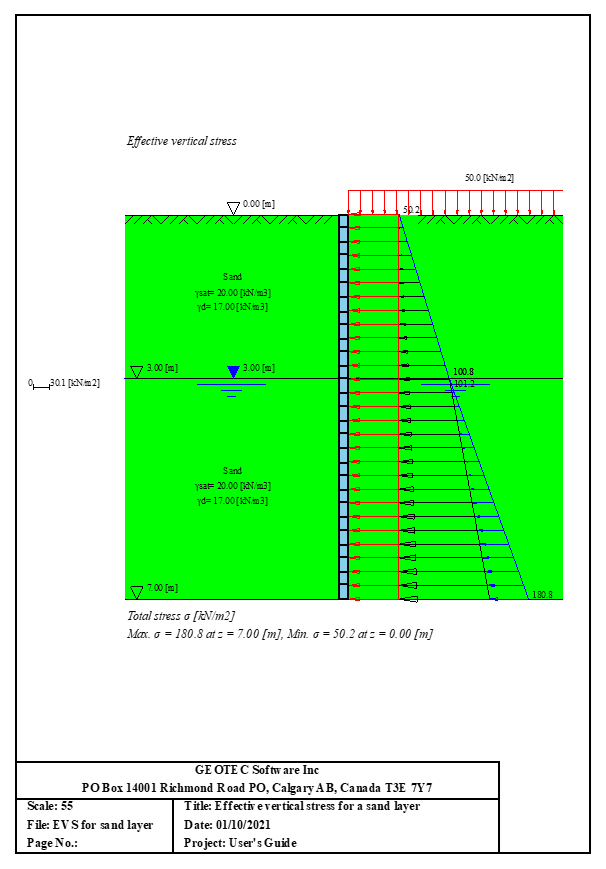
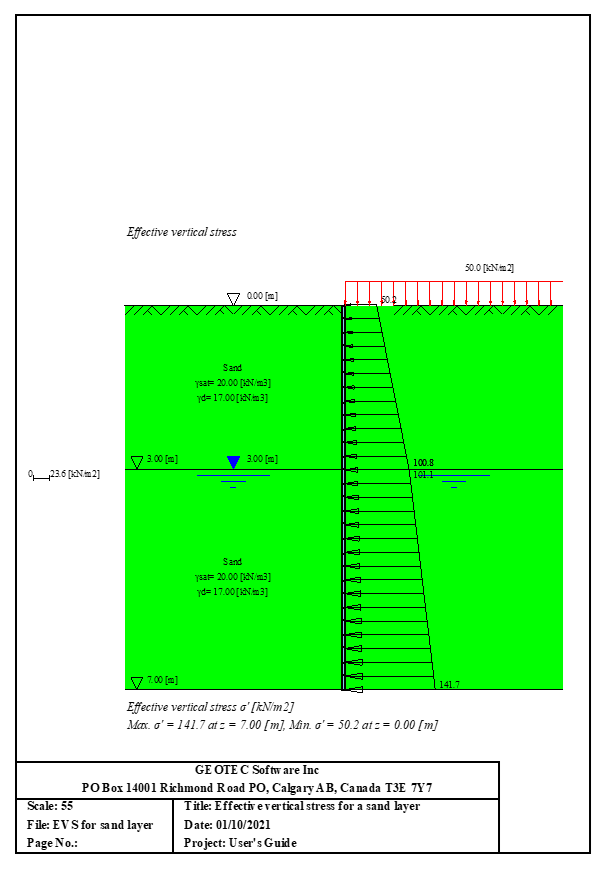
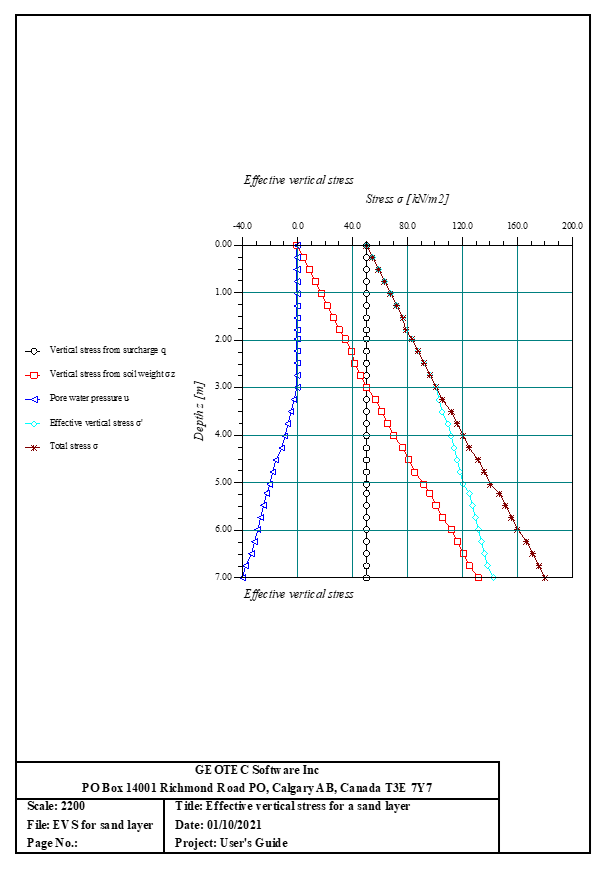
11- Berechnung von Effektiven vertikale Spannung.
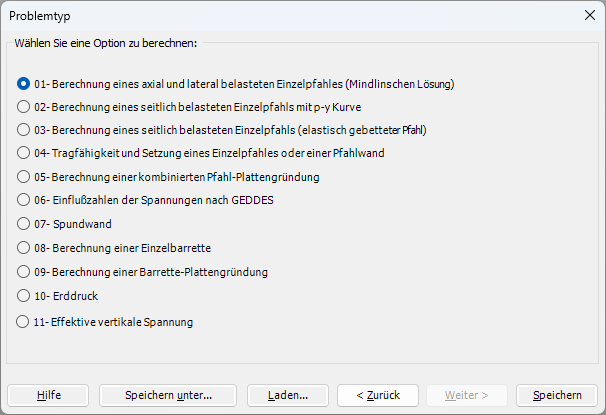
- 1- Berechnung eines axial und lateral belasteten Einzelpfahls
- 2- Berechnung eines seitlich belasteten Einzelpfahles mit p-y Kurve
- 3- Berechnung eines seitlich belasteten elastischen gebeteten Einzelpfahles
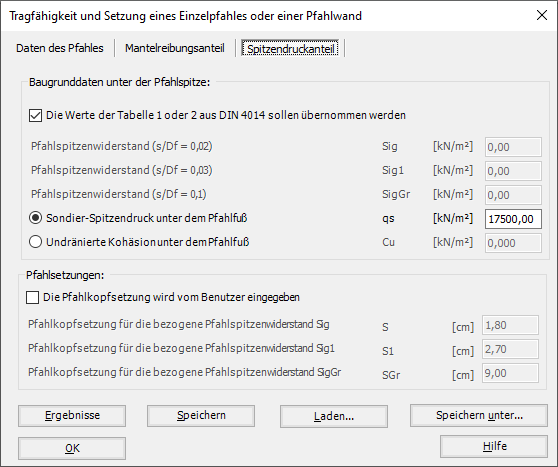
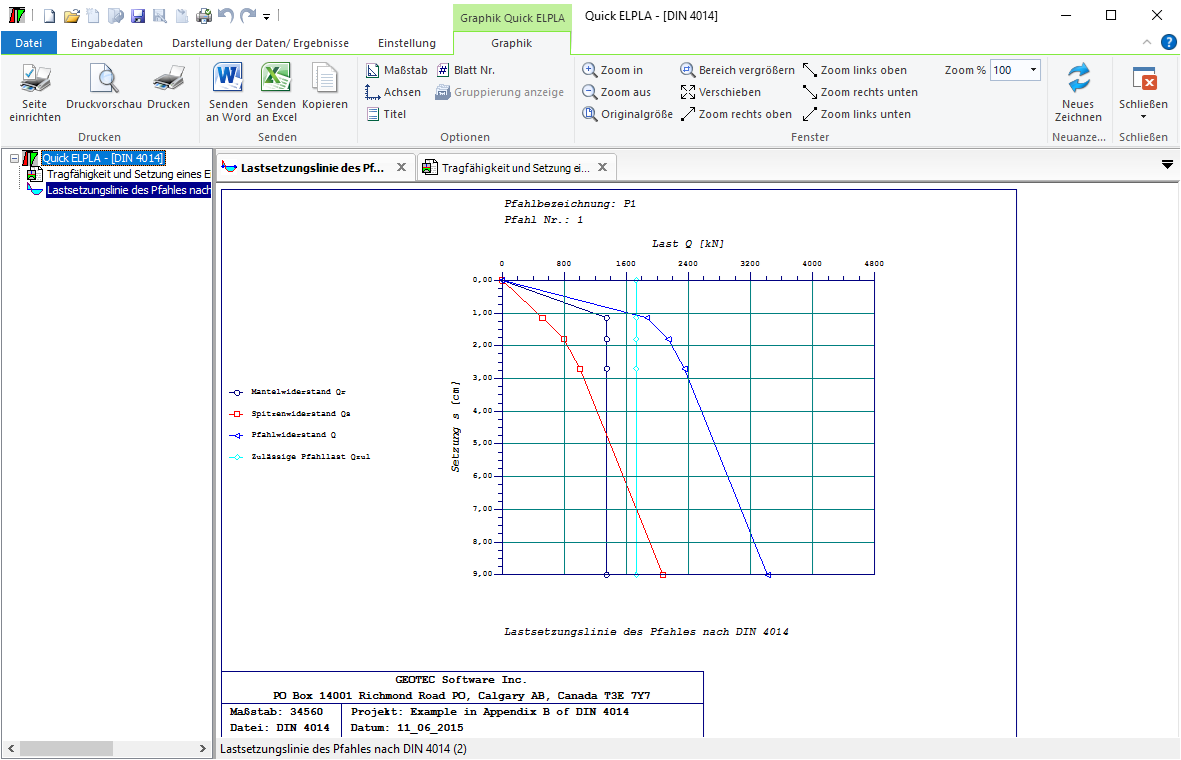
- 4 - Tragfähigkeit und Setzung eines Einzelpfahles oder einer Pfahlwand
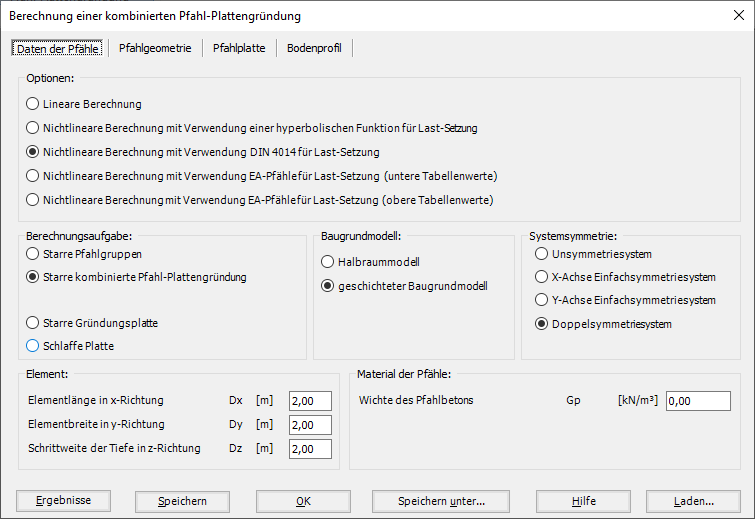
- 5- Berechnung einer Kombinierten Pfahl-Plattengründung
- 6- Einflusszahlen der Spannungen nach GEDDES
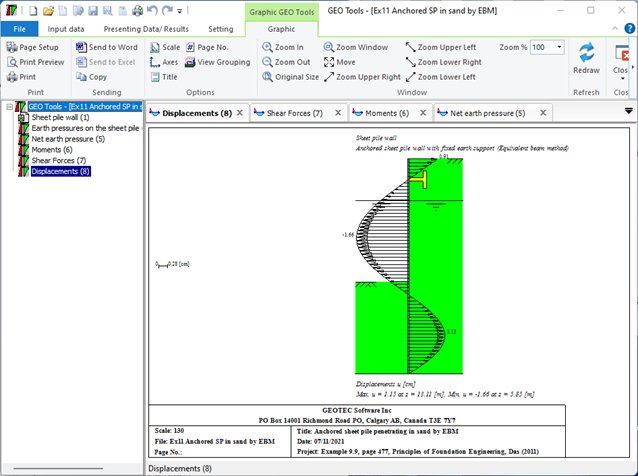
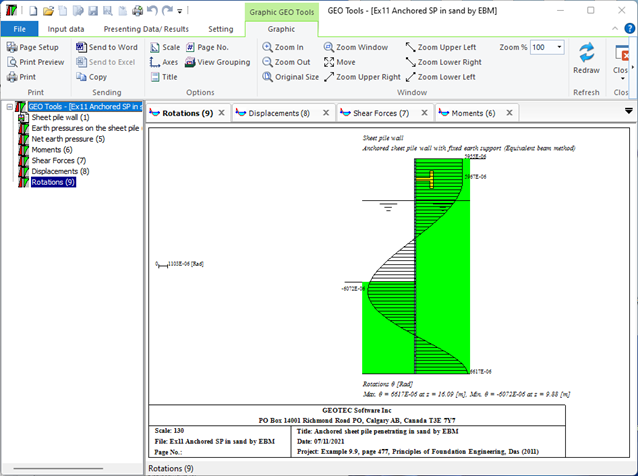
- 7- Spundwand
- 8- Berechnung einer Einzebarrette
- 9 - Berechnung einer Barrette-Plattengründung
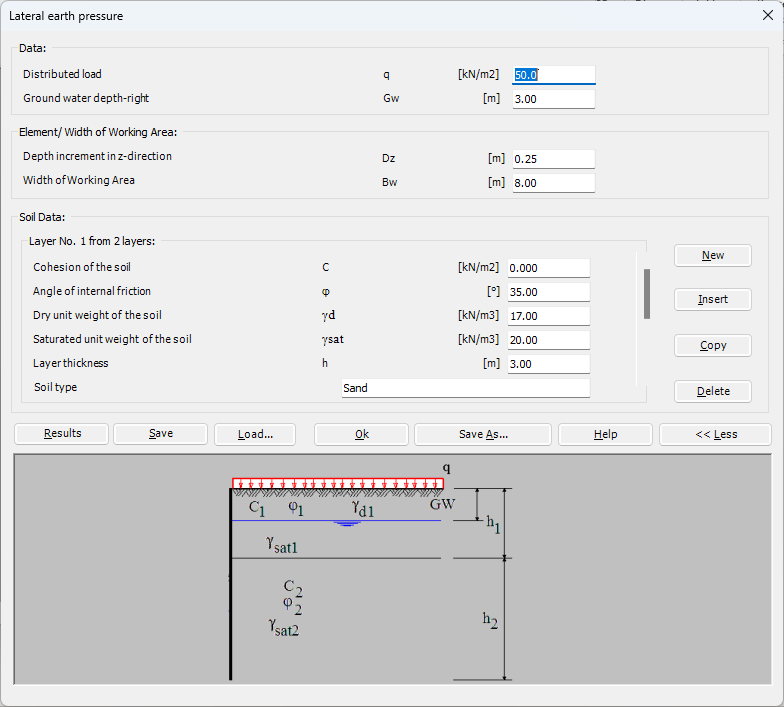
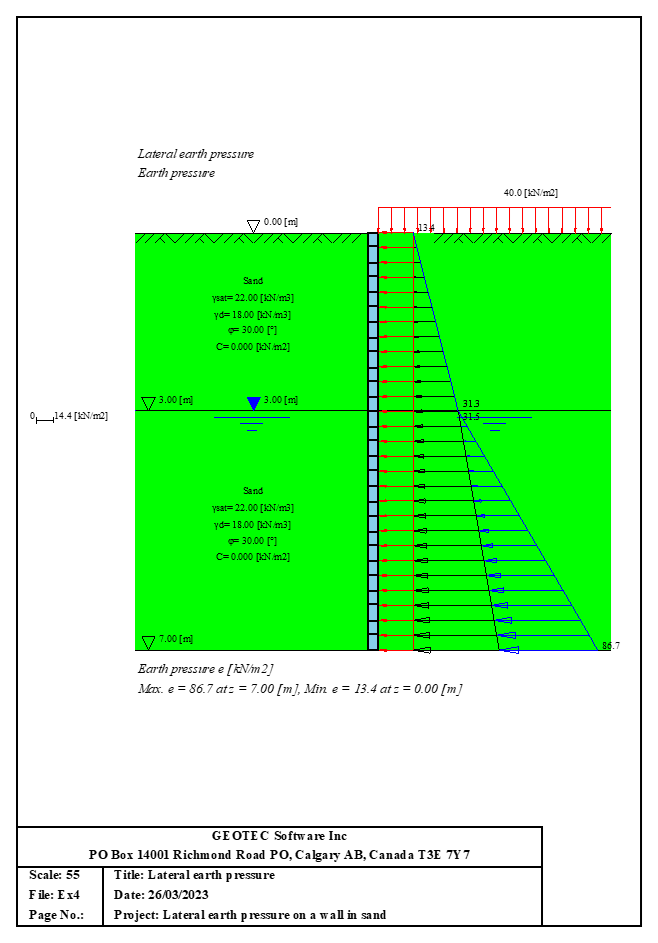
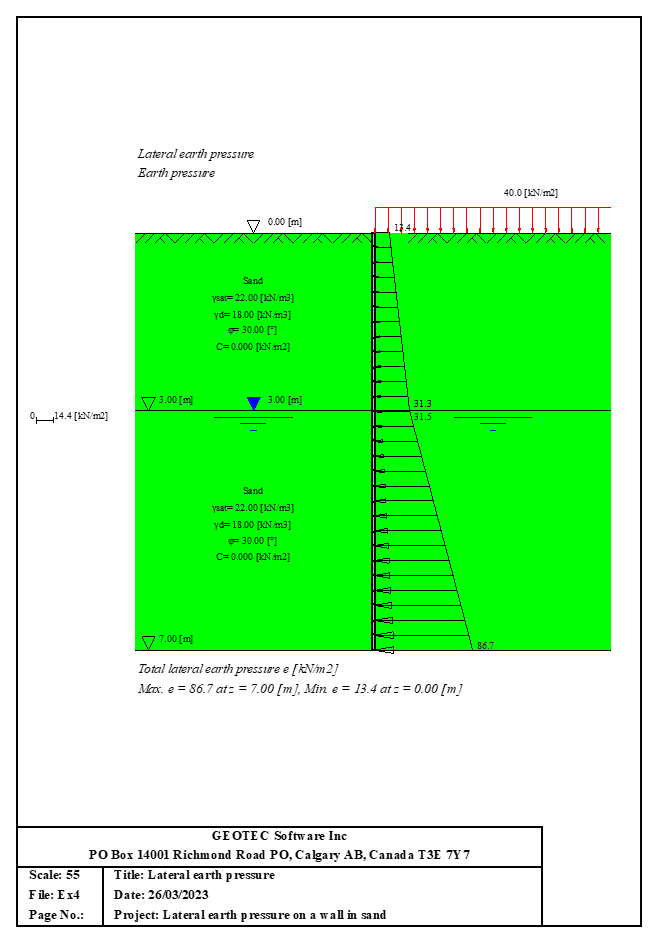
- 10- Berechnung von Erddruck
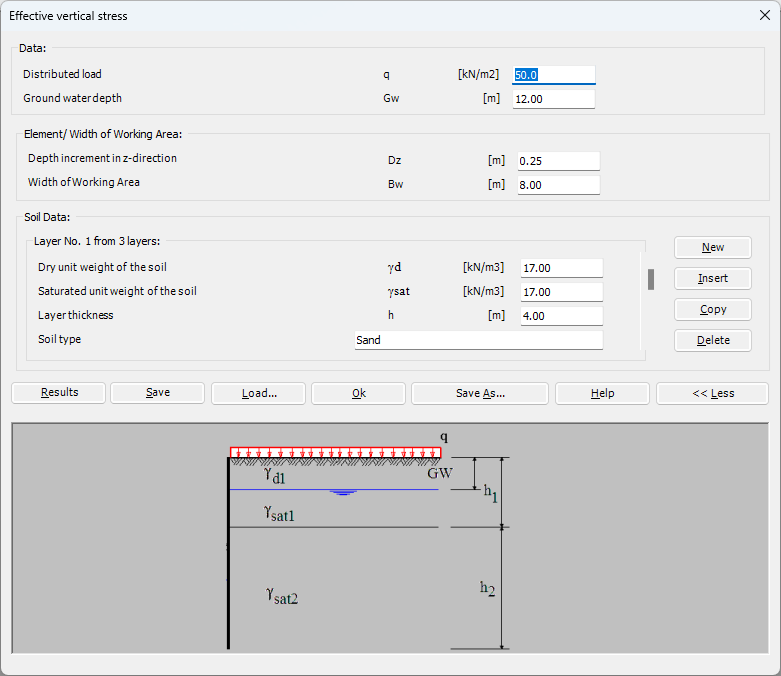
- 11- Berechnung von Effektiven vertikale Spannung
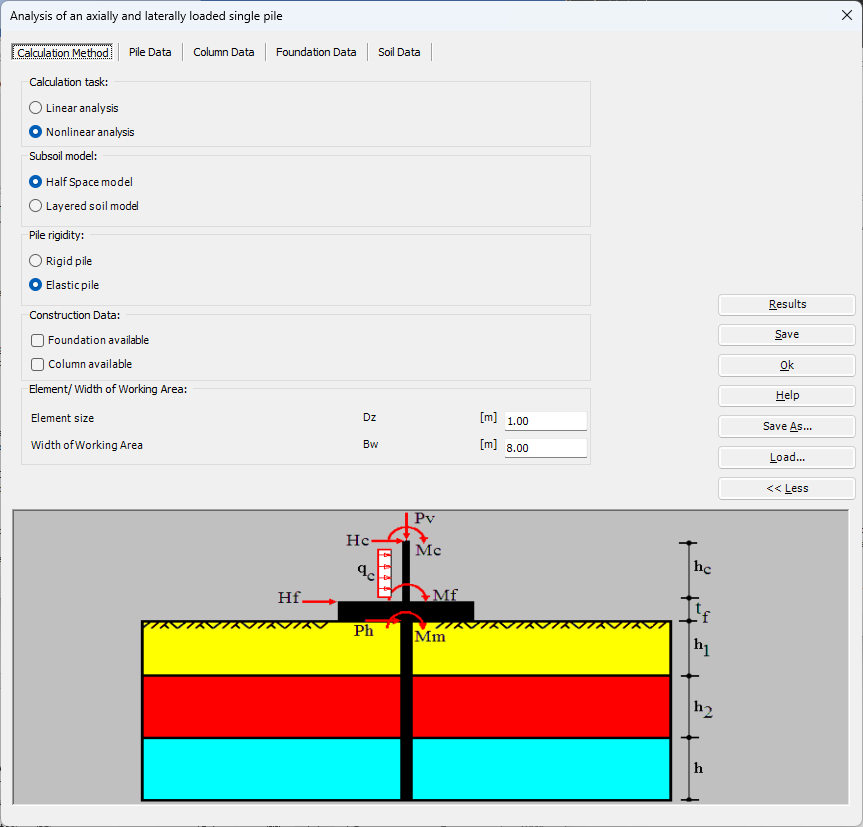
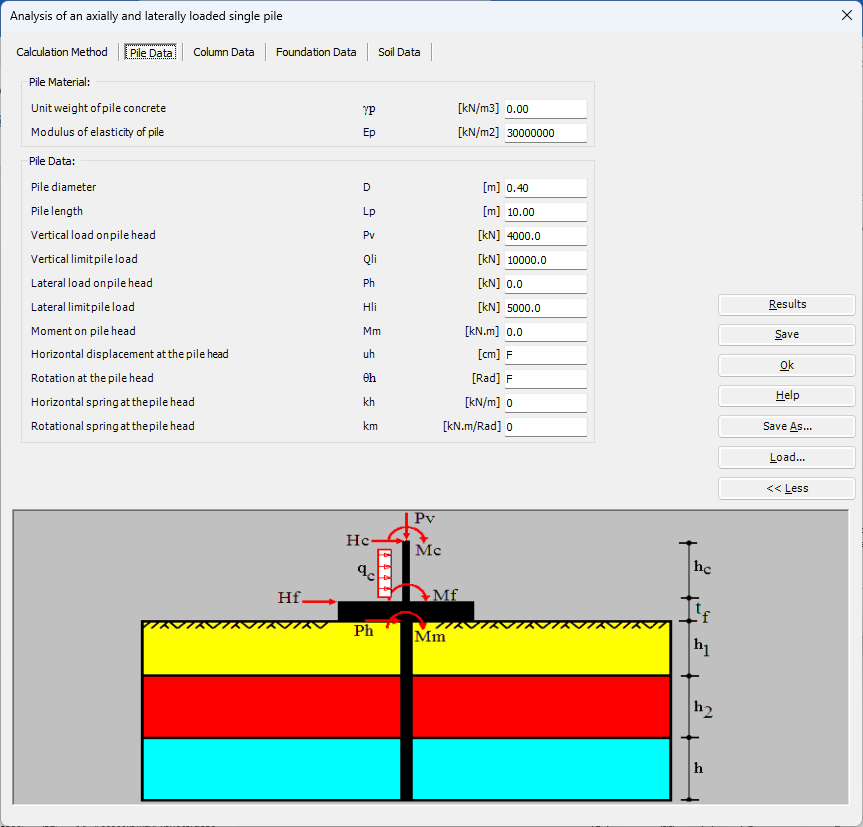
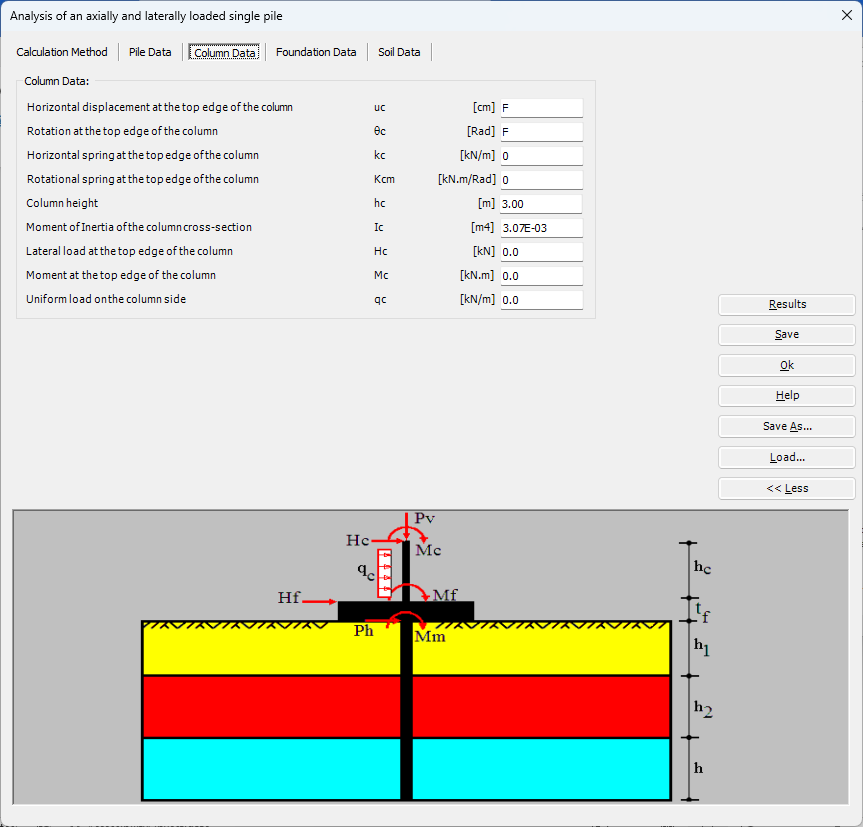
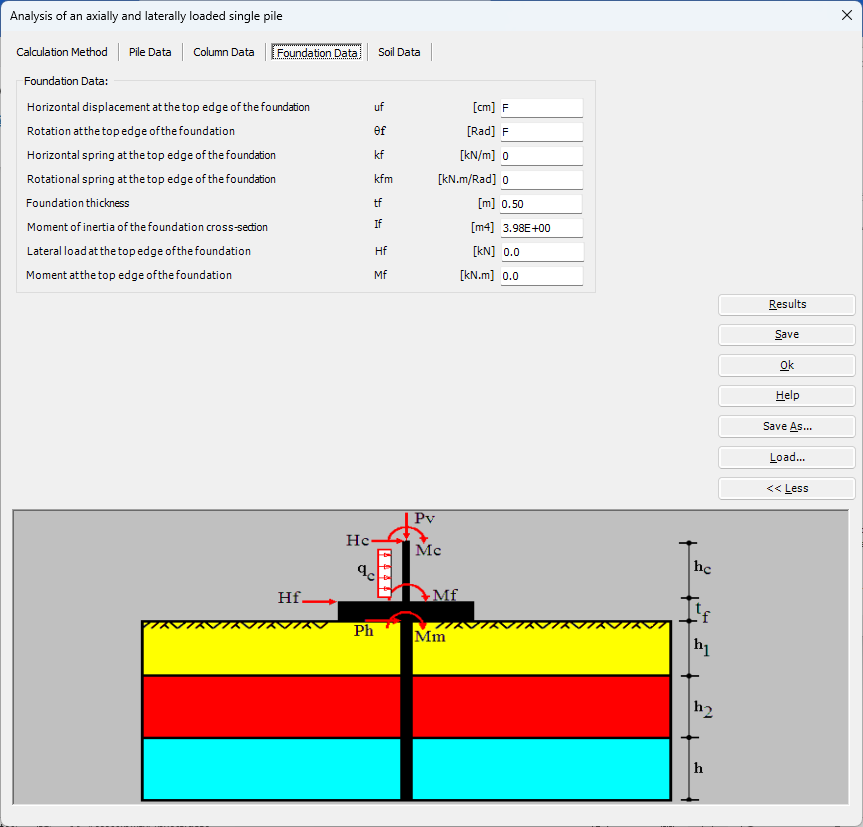
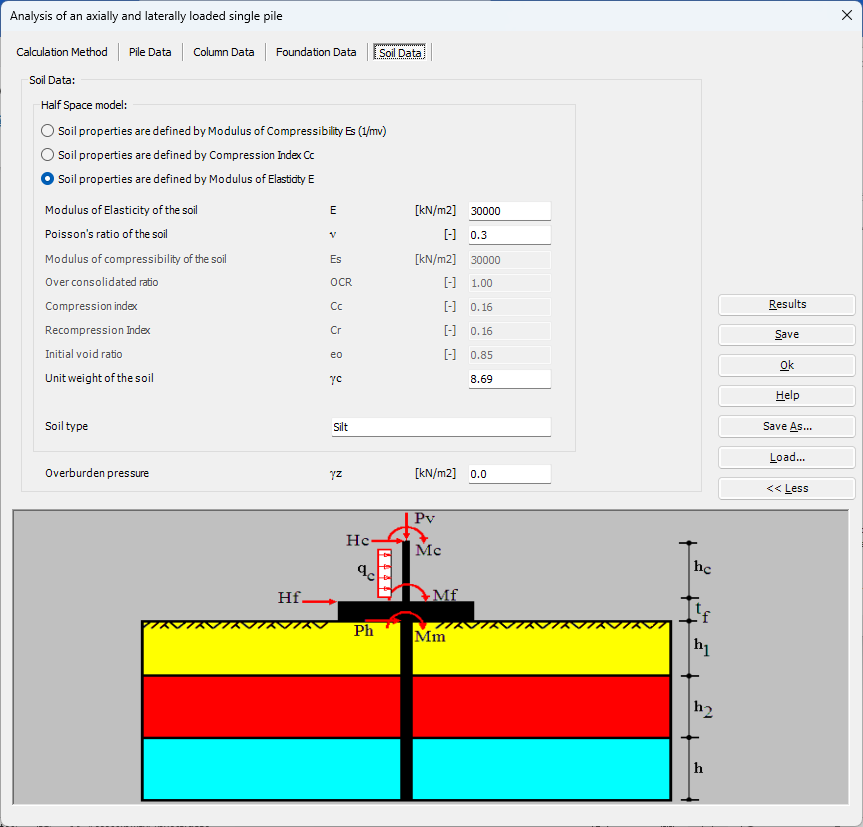
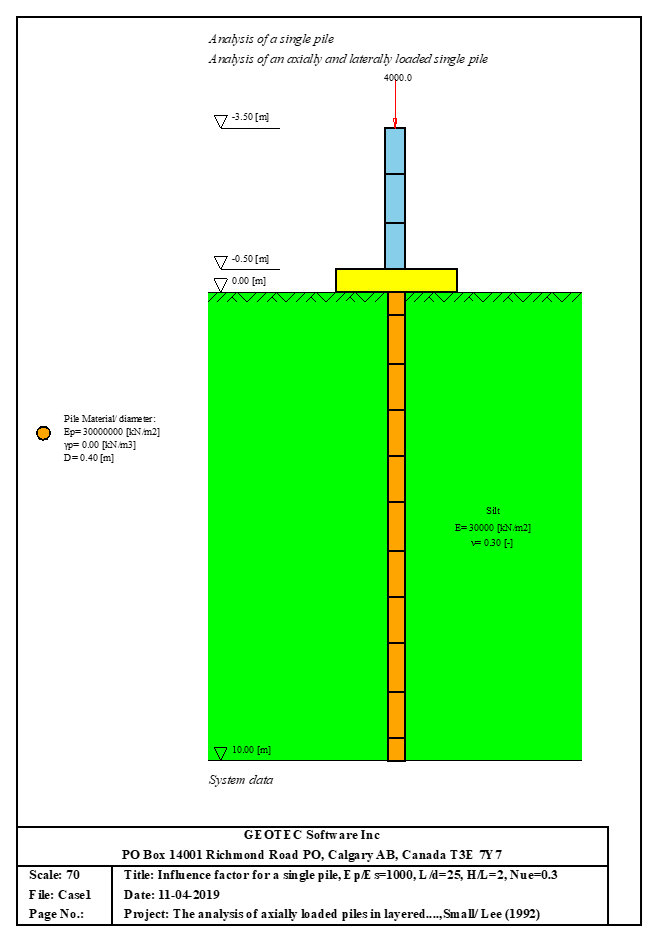
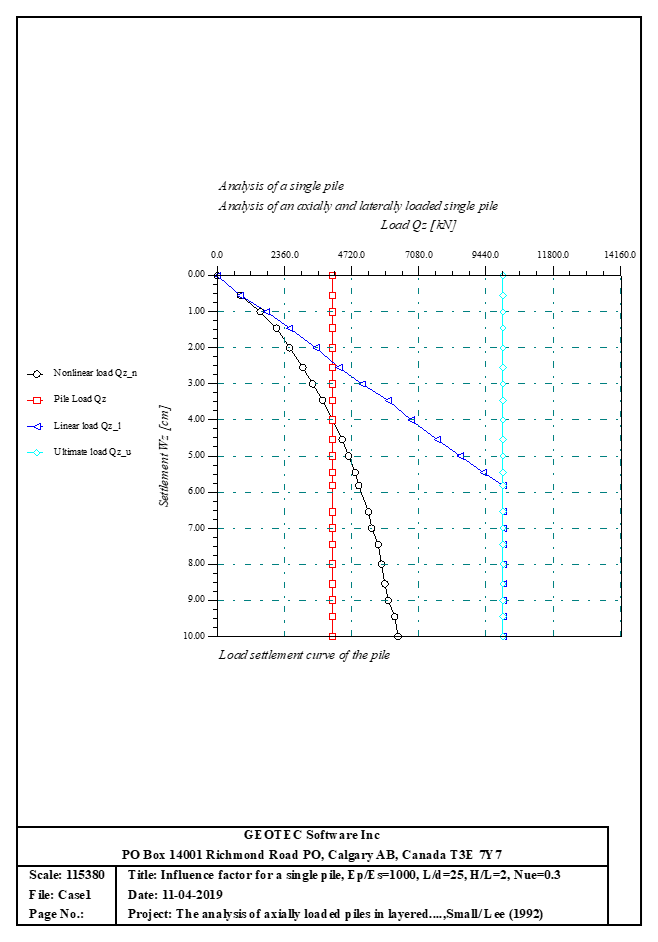
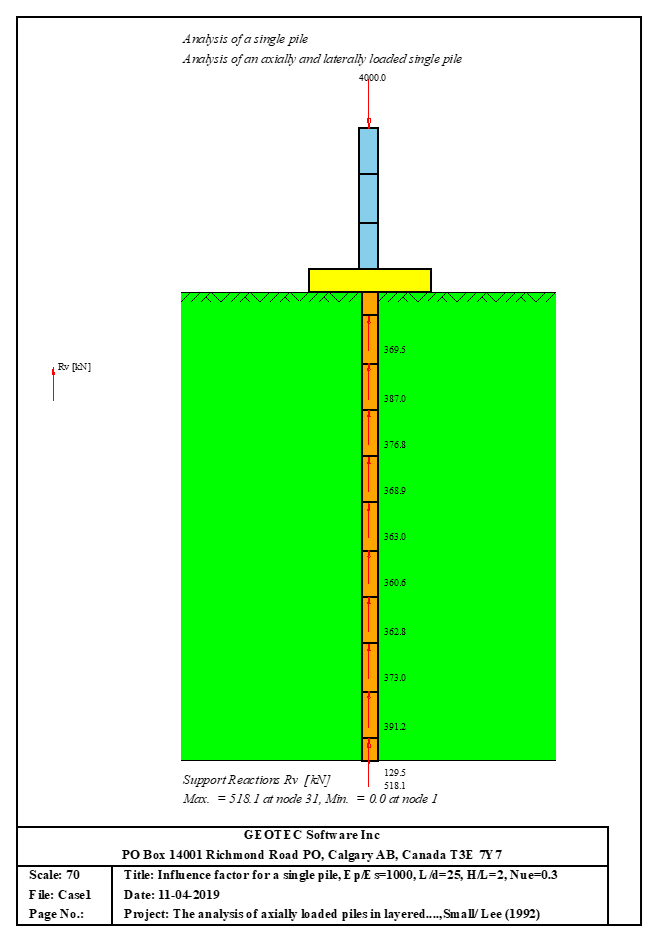
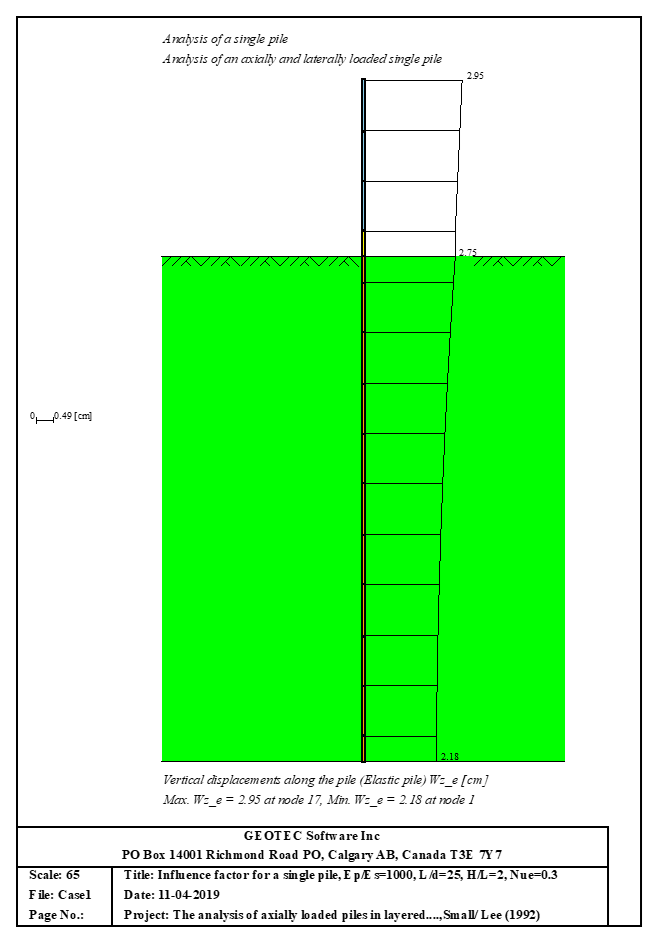
Der axial und lateral belastete Pfahl kann mit Mindlin-Lösungen analysiert werden. Der elastische Pfahl wird mit der Finite-Elemente-Methode analysiert und die Bodensteifigkeit wird aus analytischen Lösungen von Mindlin bestimmt. Durch die Definition der Grenzlast können lineare und nichtlineare Pfahlanalysen mit hyperbolischen Funktionen durchgeführt werden. Darüber hinaus könnte der Pfahl als einzelner Pfahl oder als mit (Stütze/Fundament) verbundener Pfahl analysiert werden. Darüber hinaus könnte der Pfahlkopf frei/fest oder eine andere Einschränkung sein, ebenso die Stützen- oder Fundamentkante. Berücksichtigt werden Halbraum- und Schichtbodenmodelle.
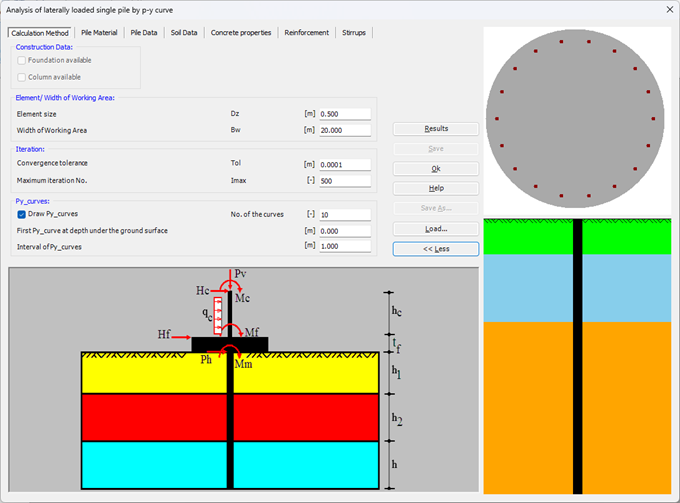
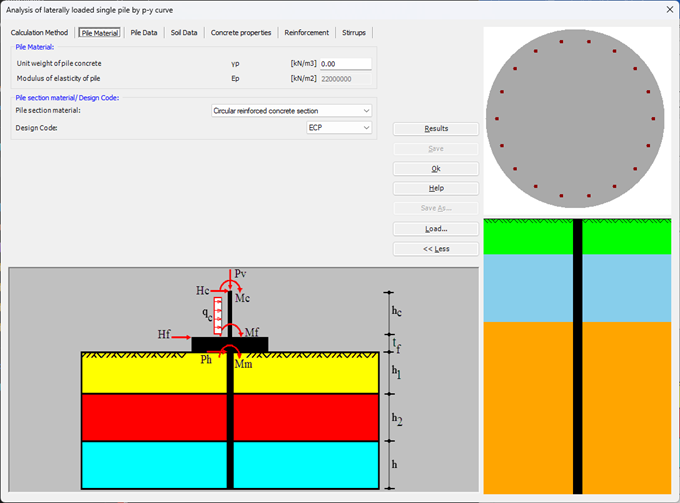
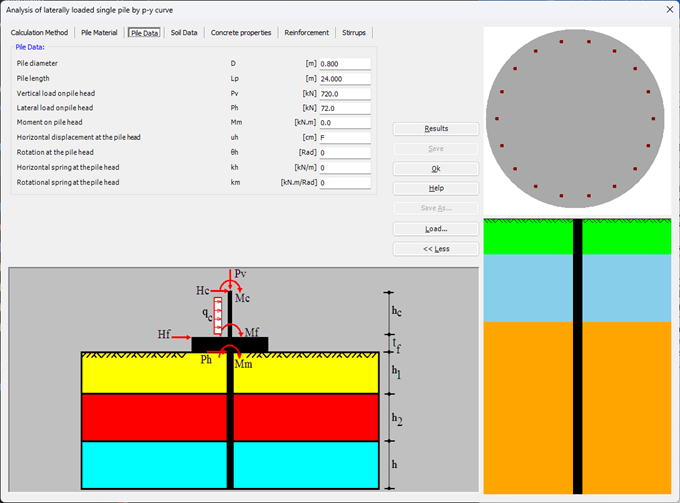
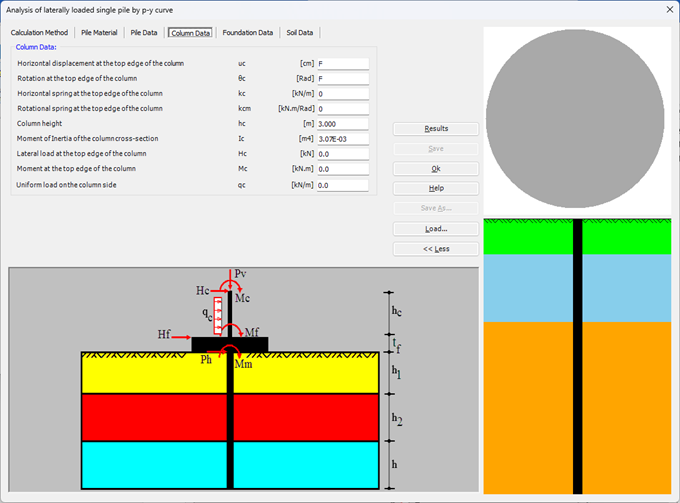
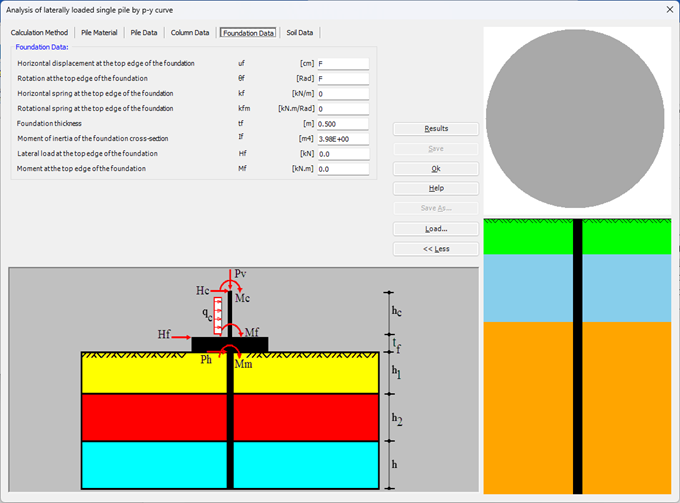
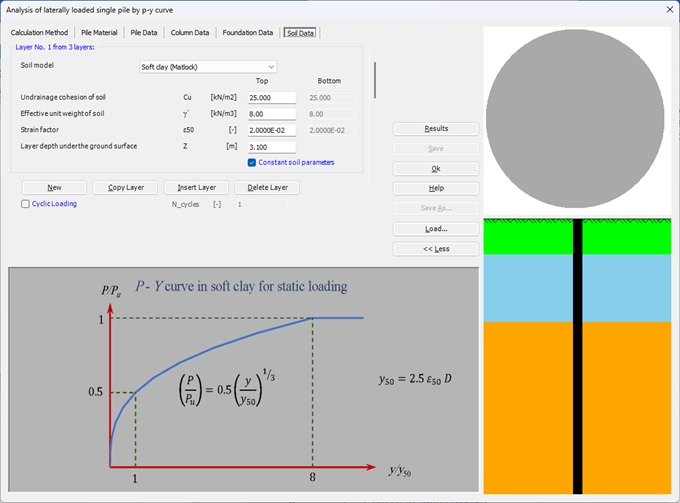
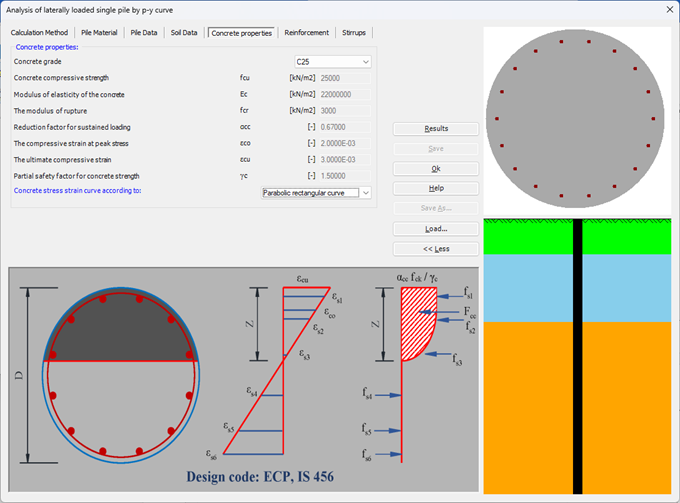
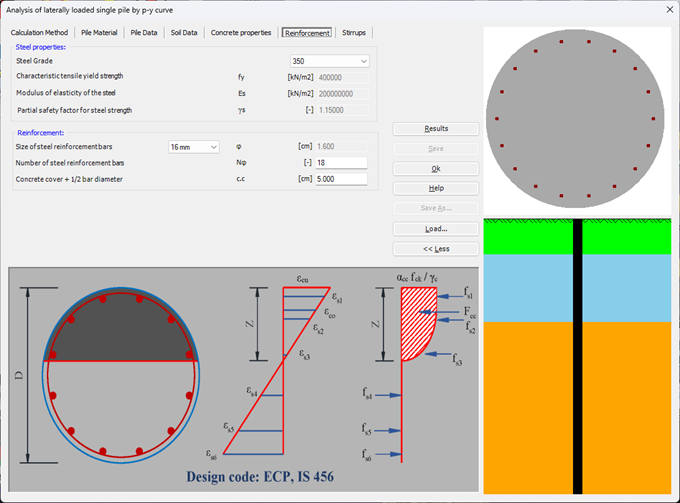
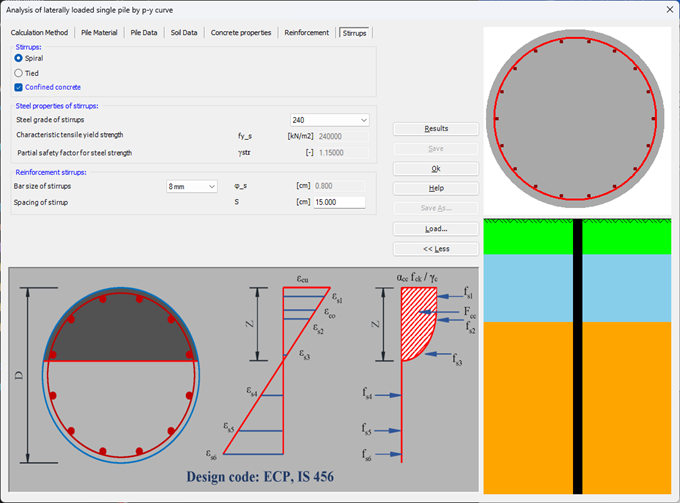
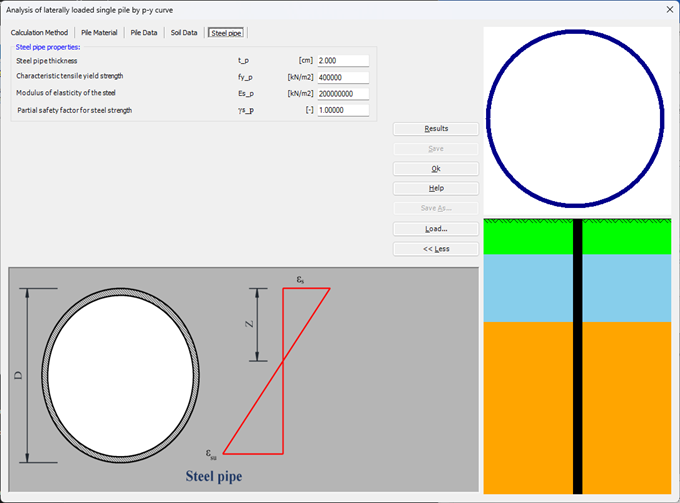
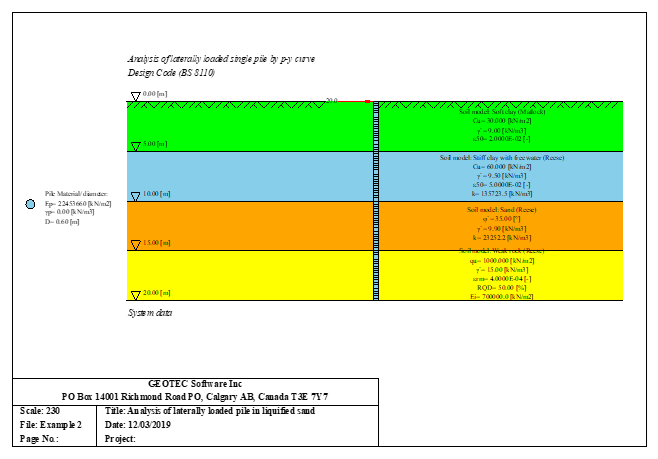
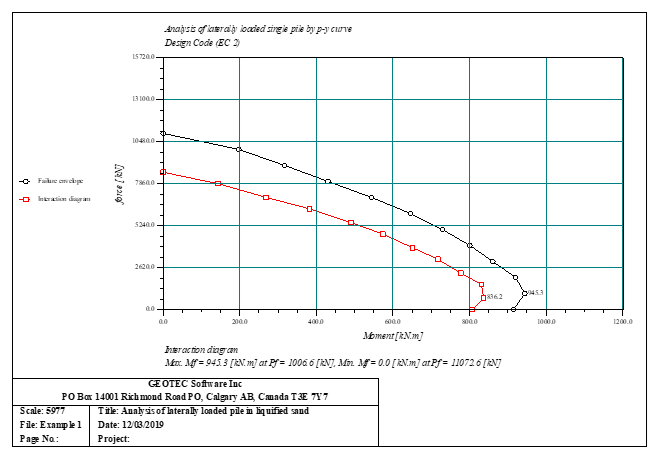
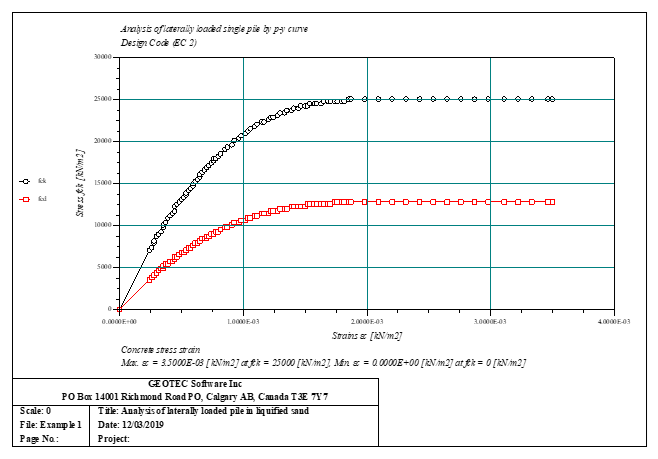
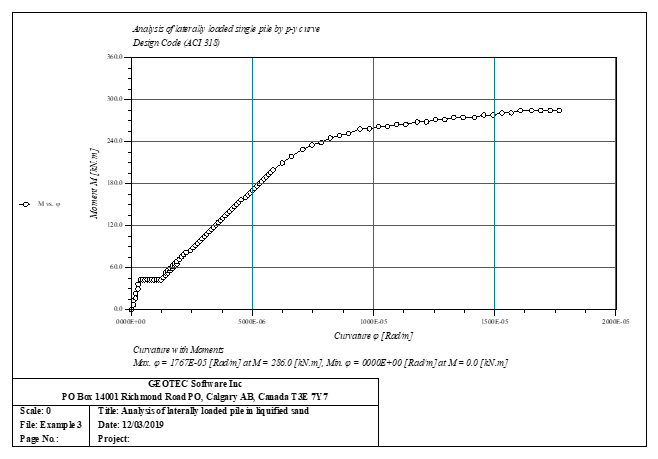
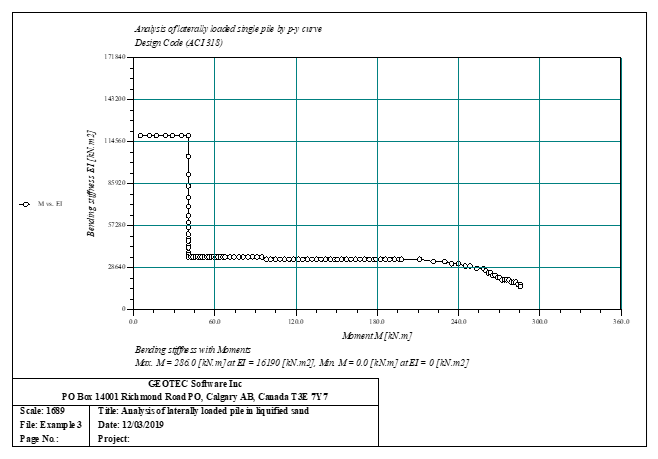
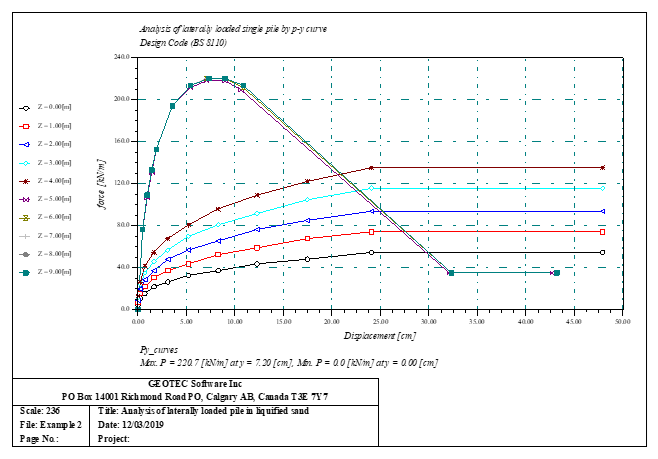
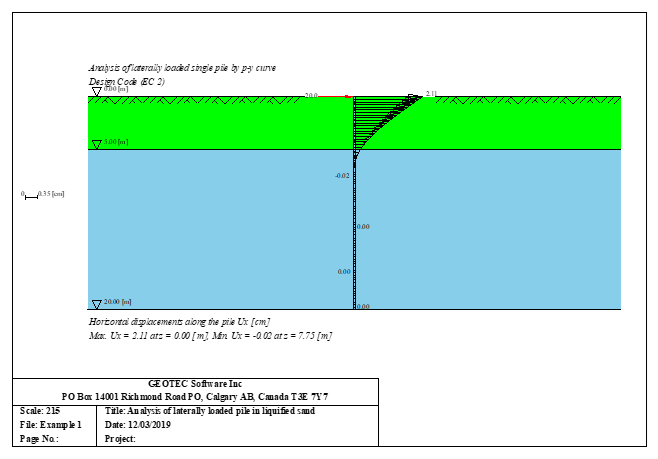
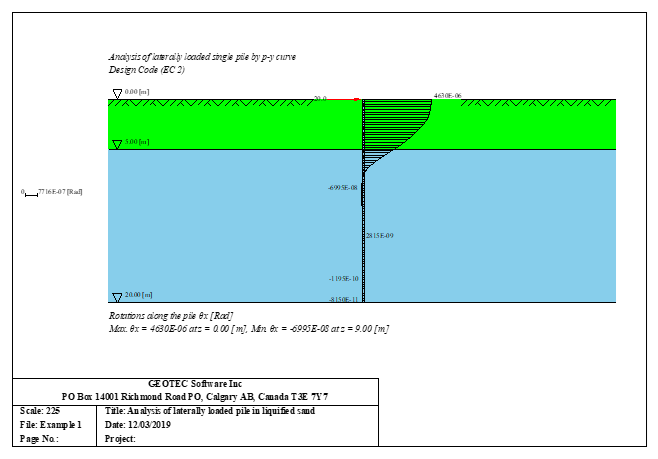
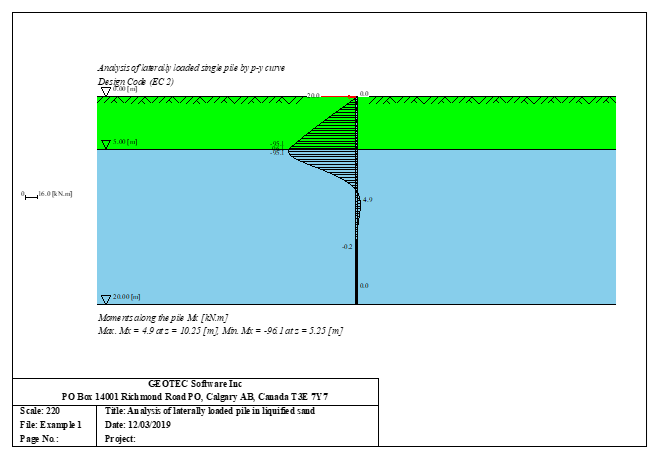

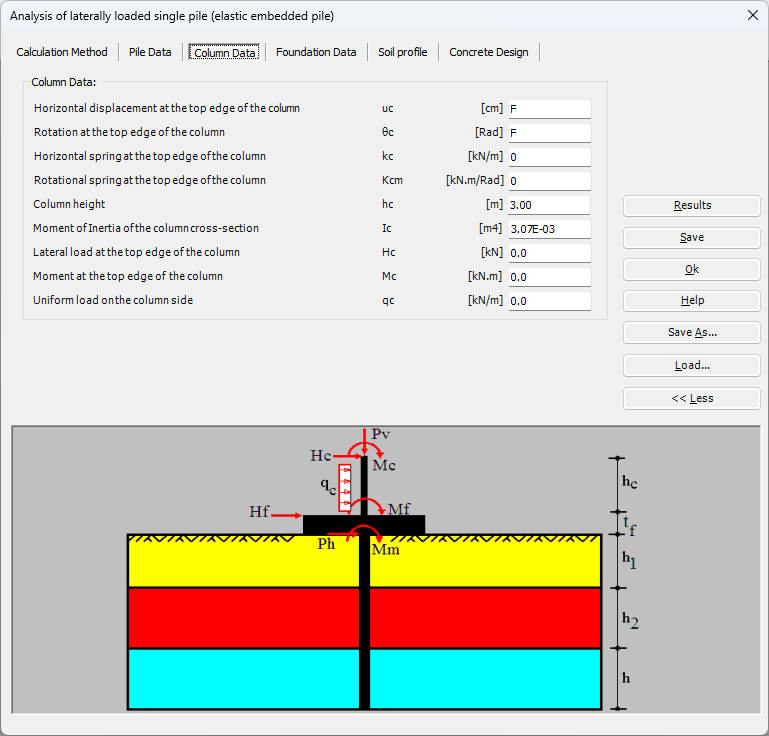
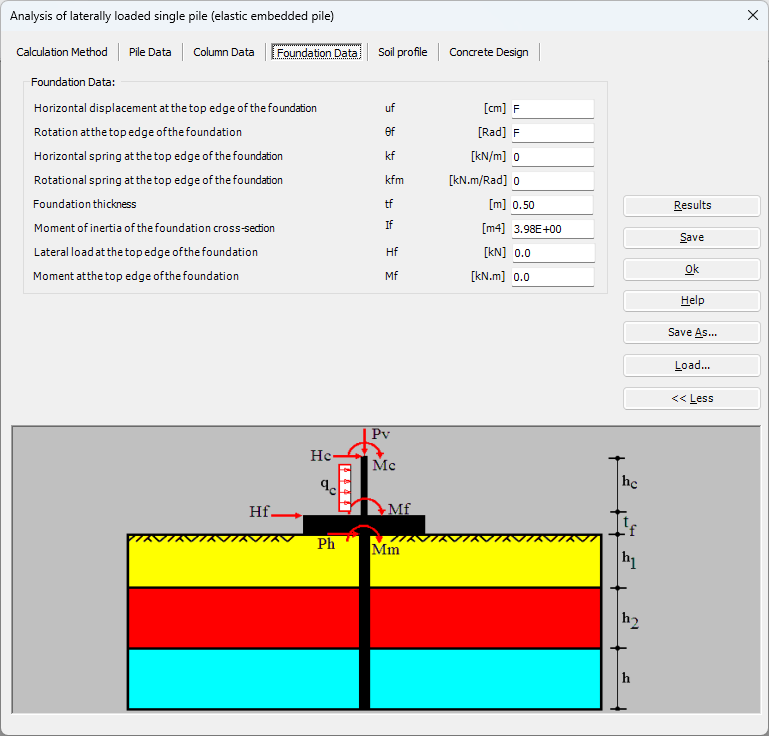
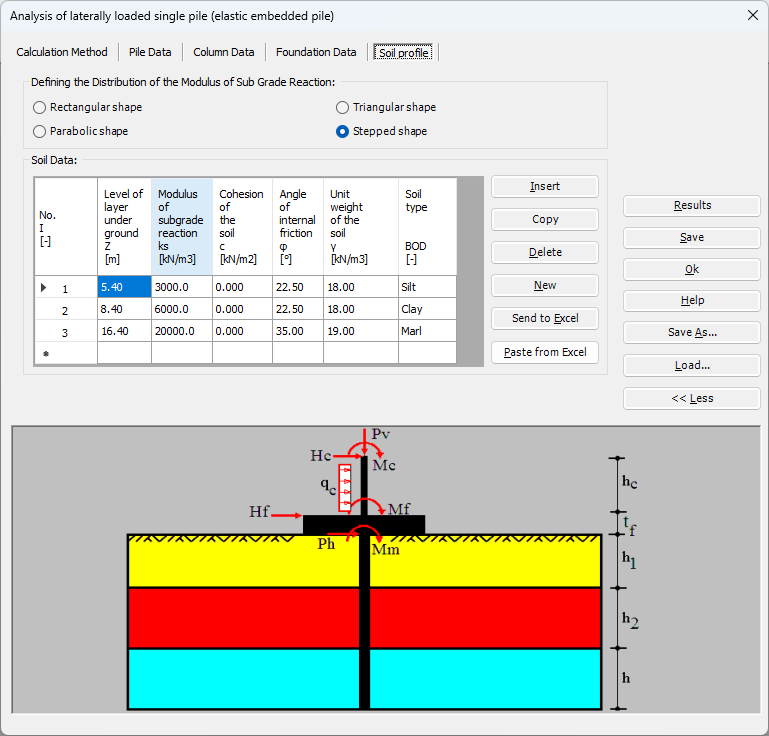
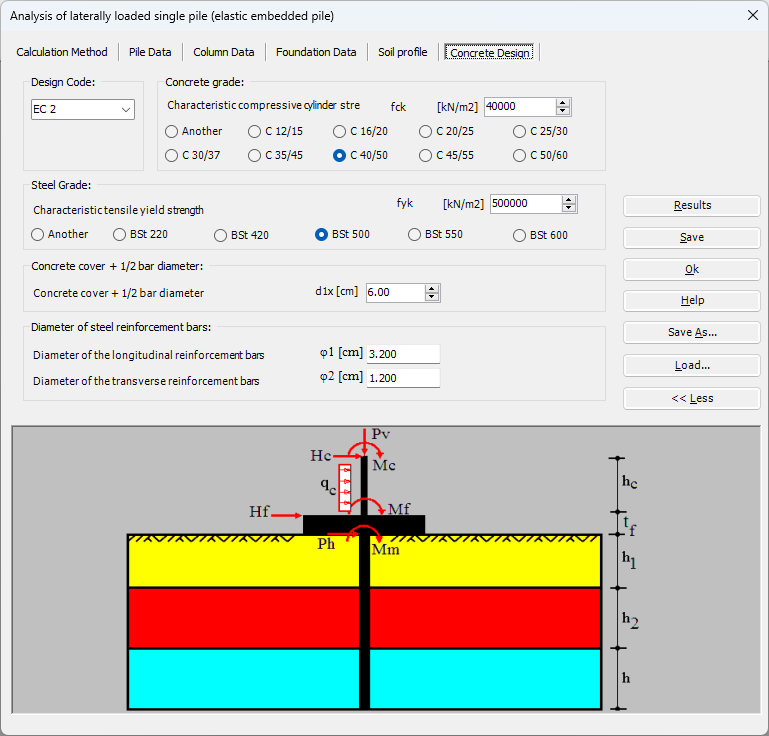
Der seitlich belastete Pfahl kann als elastisch eingebetteter Pfahl analysiert werden. Der elastische Pfahl wird mit der Finite-Elemente-Methode analysiert, und der Bettungsmodul kann nach Bowles (1997) oder durch Definition des Moduls durch den Benutzer berechnet werden. Darüber hinaus könnte der Pfahl als einzelner Pfahl oder als mit (Stütze/Fundament) verbundener Pfahl analysiert werden. Der Pfahlkopf kann frei/fest sein oder eine andere Einschränkung haben, ebenso die Stützen- oder Fundamentkante. Berücksichtigt werden Halbraum- und Schichtbodenmodelle.
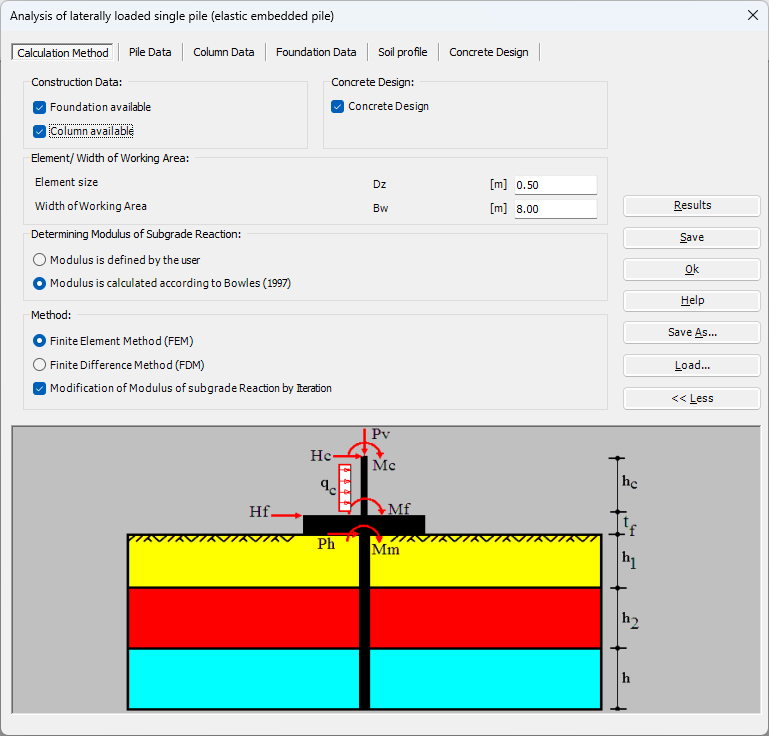
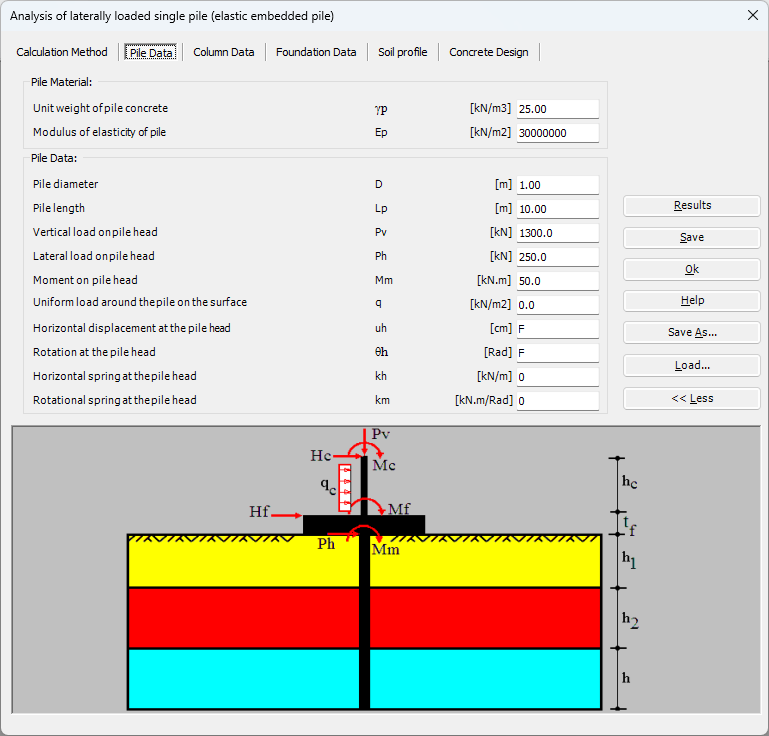
- Lineare Berechnung.
- Nichtlineare Berechnung mit Verwendung einer hyperbolischen Funktion für Last-Setzung.
- Nichtlineare Berechnung mit Verwendung DIN 4014 für Last-Setzung.
- Nichtlineare Berechnung mit Verwendung EA-Pfähle für Last-Setzung (untere Tabellenwerte).
- Nichtlineare Berechnung mit Verwendung EA-Pfähle für Last-Setzung (obere Tabellenwerte).
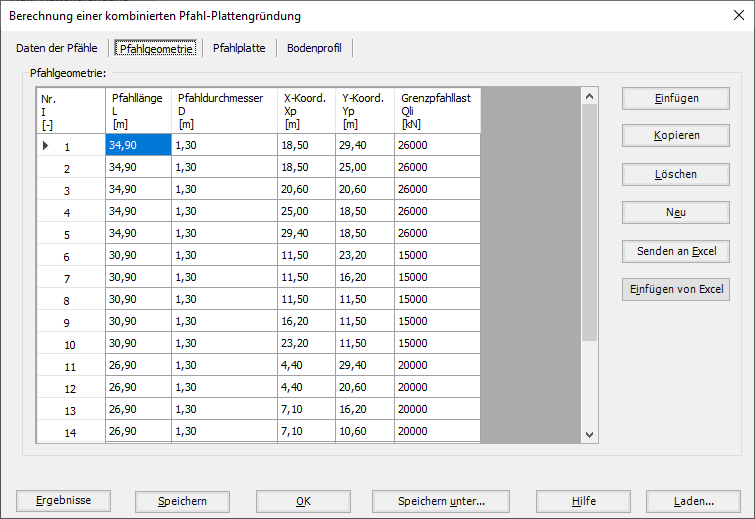
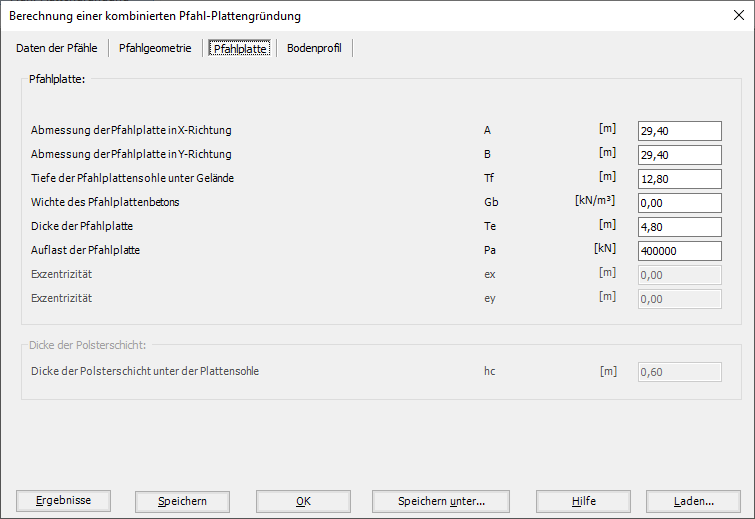
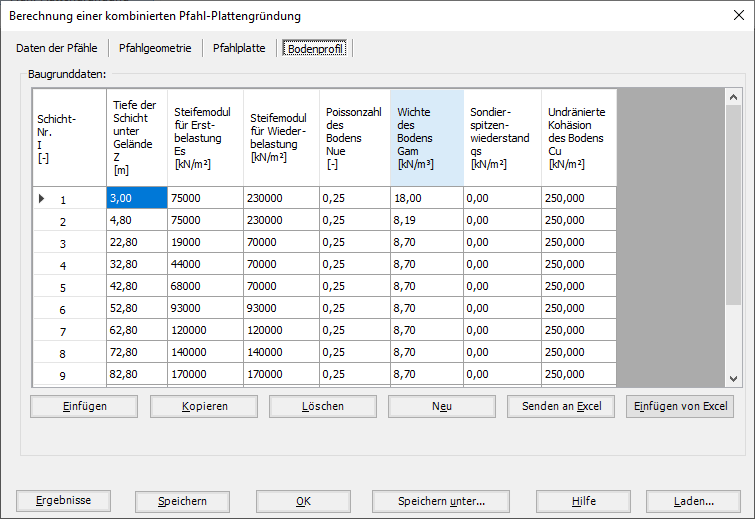
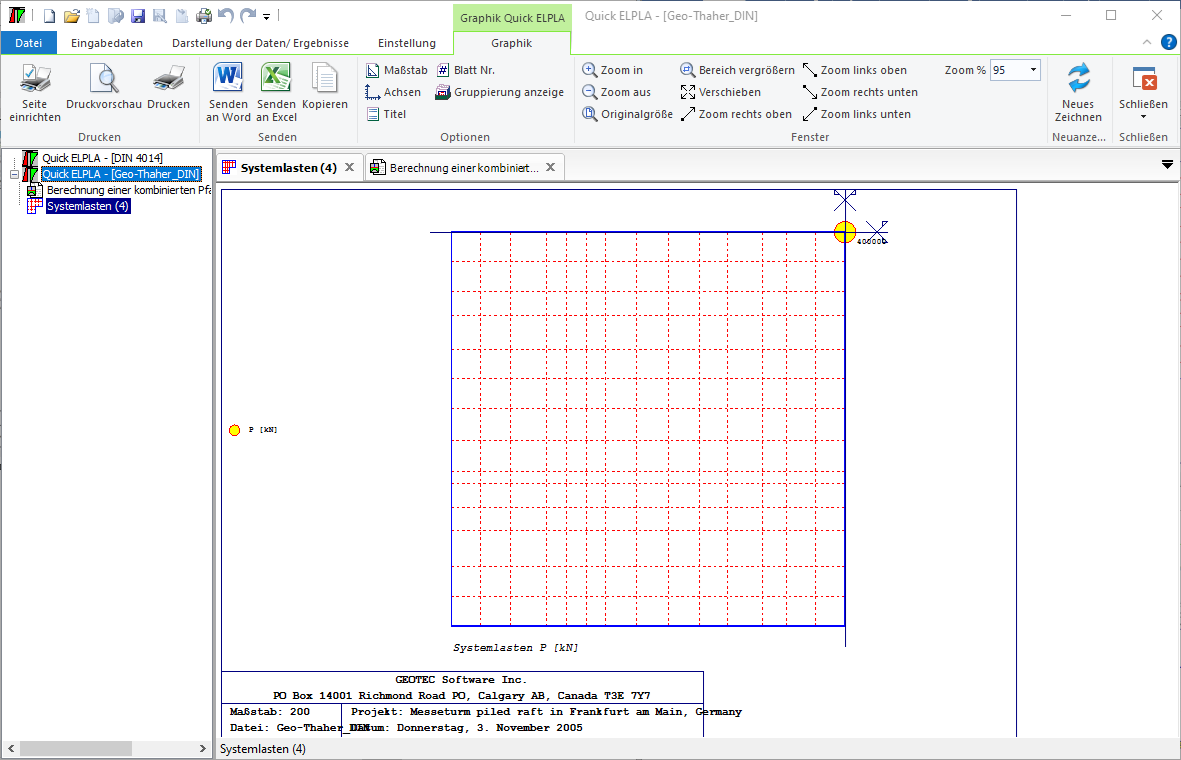
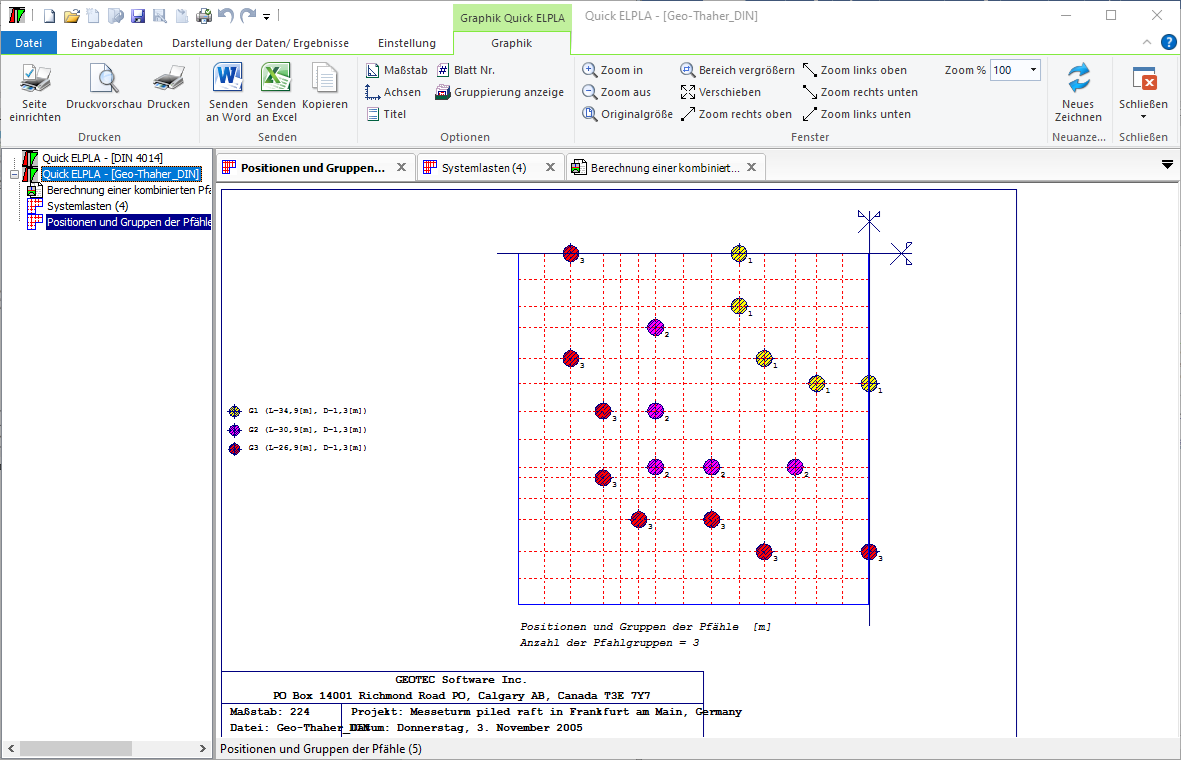
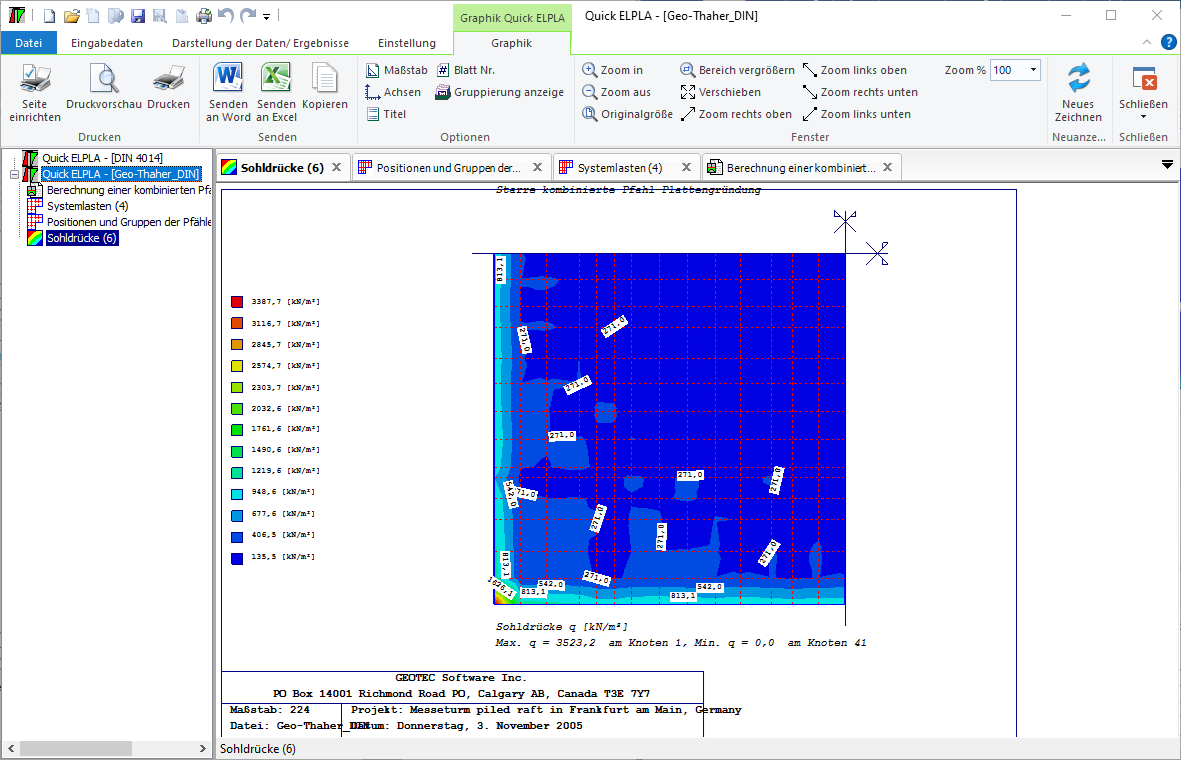
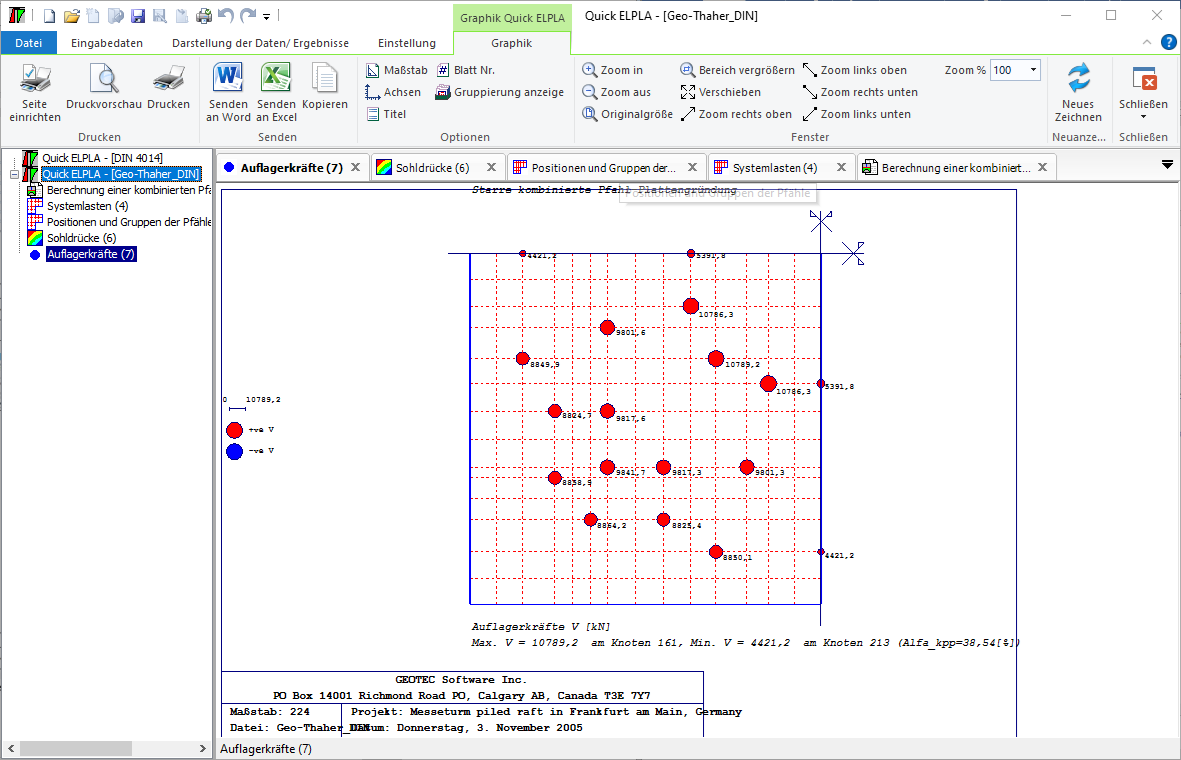
Es werden drei Lastarten berücksichtigt:
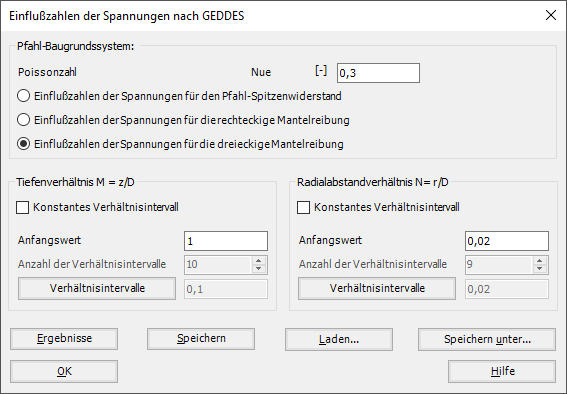
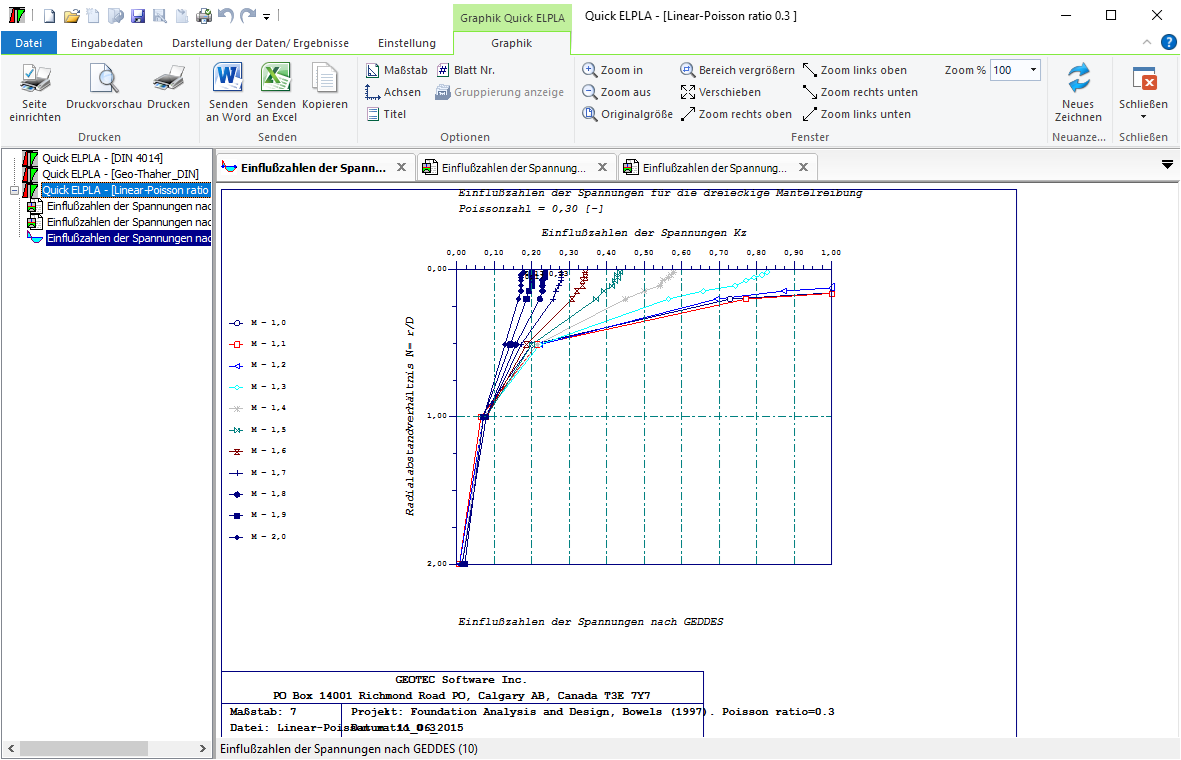
- Einflusszahlen der Spannungen für den Pfahl-Spitzenwiderstand.
- Einflusszahlen der Spannungen für die rechteckige Mantelreibung.
- Einflusszahlen der Spannungen für die dreieckige Mantelreibung.
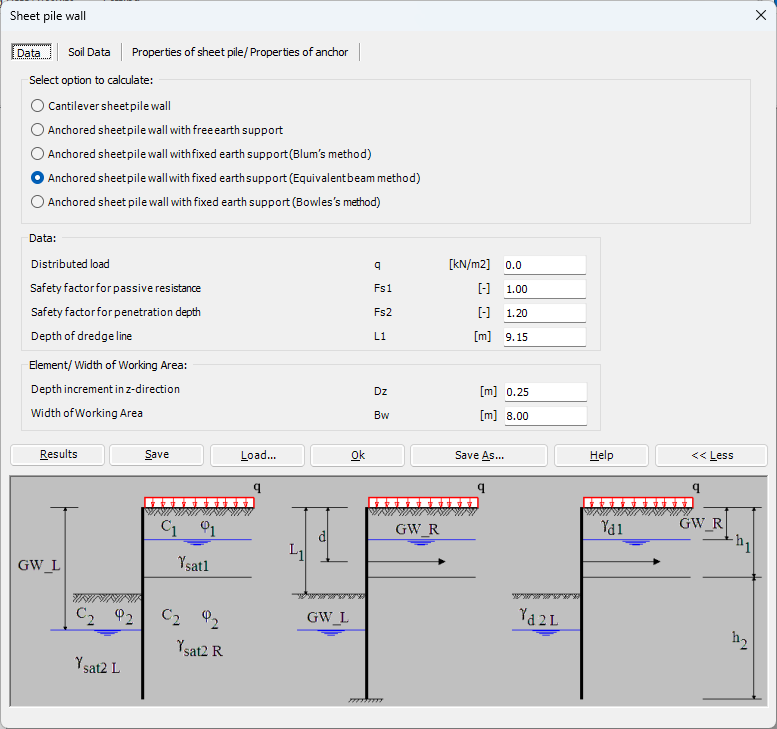
Um eine LEA-Analyse für eine Spundwand durchzuführen, werden typischerweise die folgenden Schritte befolgt:
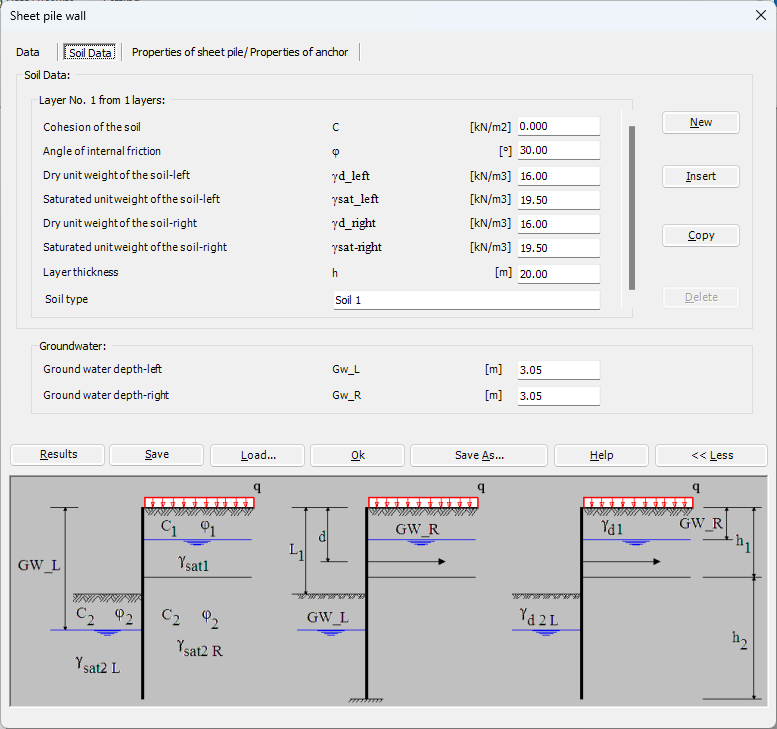
- Bestimmen Sie die Bodeneigenschaften: Der erste Schritt der Analyse besteht darin, die Bodeneigenschaften zu bestimmen, einschließlich Bodentyp, Festigkeit und Steifigkeit. Diese Informationen werden zur Berechnung des auf die Spundwand wirkenden Bodendrucks verwendet.
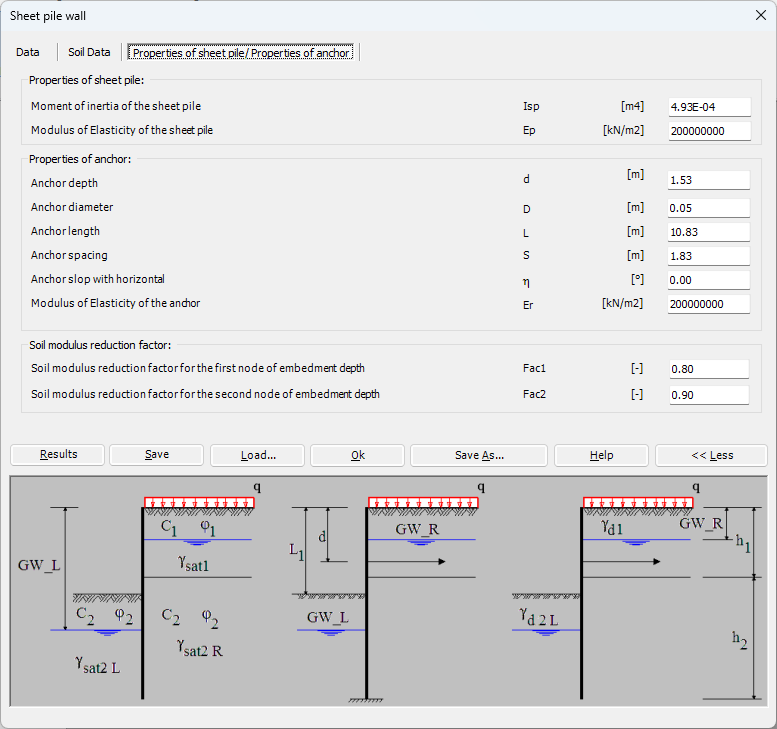
- Definieren Sie die Ladebedingungen: Der nächste Schritt besteht darin, die Ladebedingungen zu definieren, einschließlich etwaiger externer Lasten und des Wasserstands. Aus diesen Informationen werden die auf die Spundwand wirkenden Kräfte und Momente berechnet.
- Berechnen Sie die Kräfte und Momente: Anhand der Bodeneigenschaften und Belastungsbedingungen werden die auf die Spundwand wirkenden Kräfte und Momente berechnet. Dazu gehört der Bodendruck, der Wasserdruck und etwaige äußere Belastungen.
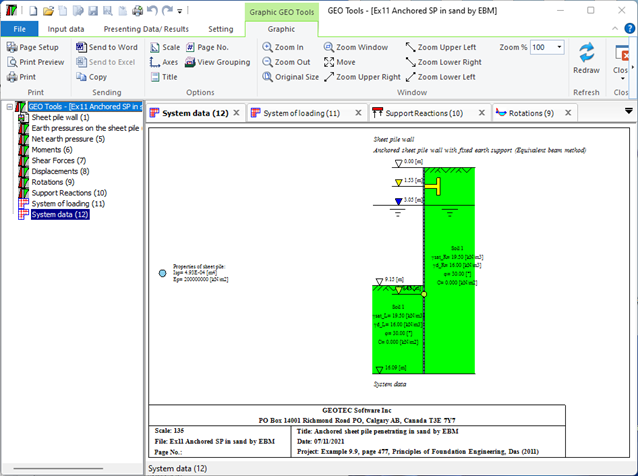
- Stabilität bewerten: Der letzte Schritt besteht darin, die Stabilität der Spundwand zu bewerten. Dazu werden die auf die Wand wirkenden Kräfte und Momente mit seiner Fähigkeit, diesen Belastungen standzuhalten, verglichen. Wenn der Wand stabil ist, ist die Analyse abgeschlossen. Andernfalls sind möglicherweise Änderungen am Design erforderlich.
- Krag-Spundwand: Dies ist eine Art Stützmauer, die aus ineinandergreifenden Stahl-, Beton- oder Holzspundwänden besteht, die in den Boden gerammt werden. Die Wände sind so konzipiert, dass sie als Ausleger fungieren und auf einer Seite dem seitlichen Druck von Erde und Wasser standhalten, während sie auf der anderen Seite vom Boden gestützt werden.
- Verankerte Spundwand mit freier aufgelagerter Wand: Diese Art von Stützmauer ähnelt der freitragenden Spundwand, verfügt jedoch über zusätzliche Unterstützung in Form von Ankern, die im Boden hinter der Wand installiert werden. Die Anker bieten zusätzlichen Widerstand gegen den seitlichen Druck von Boden und Wasser.
- Verankerte Spundwand mit eingespannter aufgelagerter Wand (Blum-Methode): Bei dieser Art von Stützmauer werden die Spundwände an einem starren Strukturelement wie einem Betonbalken oder einer Betonplatte verankert. Das Strukturelement fungiert als feste Stütze und verhindert, dass sich die Spundwände nach innen durchbiegen.
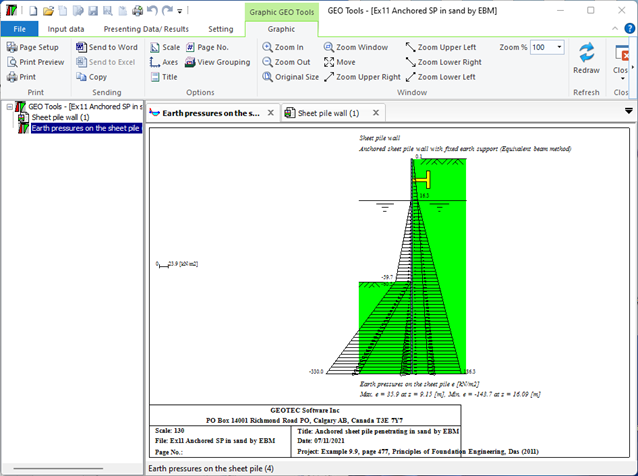
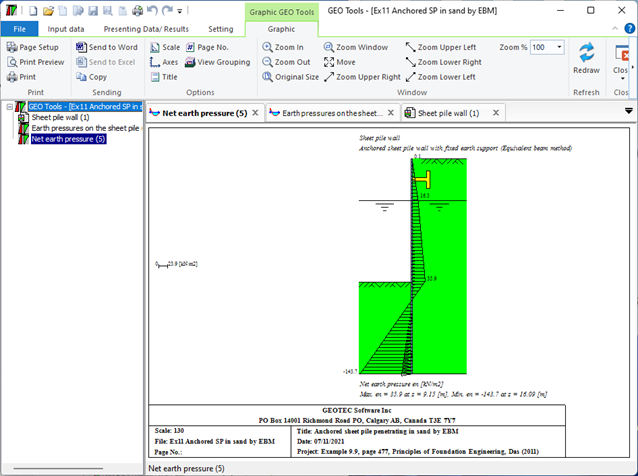
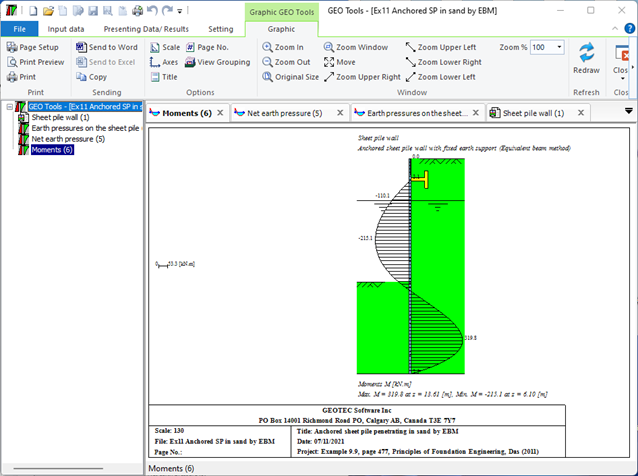
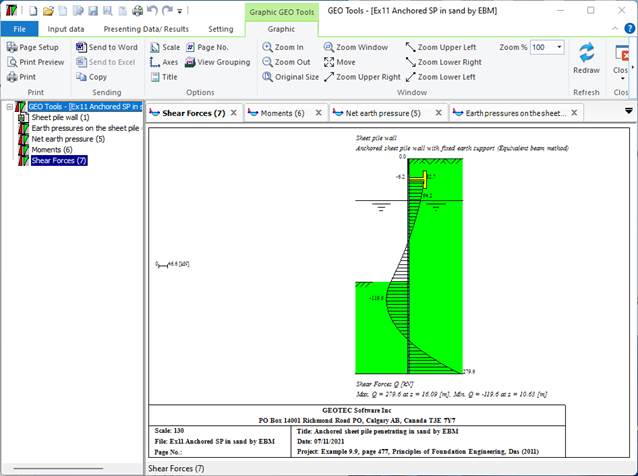
- Verankerte Spundwand mit eingespannter aufgelagerter Wand (Äquivalentbalkenmethode): Bei dieser Methode wird die Spundwand als Ersatzbalken behandelt und die auf sie einwirkenden Kräfte analysiert. Das feste Ende des Balkens ist an einer starren Struktur verankert, während das freie Ende vom Boden getragen wird. Mithilfe der Analyse werden die erforderliche Größe und der Abstand der Anker ermittelt.
- Verankerte Spundwand mit eingespannter aufgelagerter Wand (Bowles-Methode): Diese Methode ähnelt der äquivalenten Balkenmethode, berücksichtigt jedoch auch den auf die Spundwand wirkenden Bodenwiderstand. Die Analyse umfasst die Berechnung des auf die Spundwände wirkenden Biegemoments und der Querkräfte sowie die entsprechende Auslegung des Ankersystems.
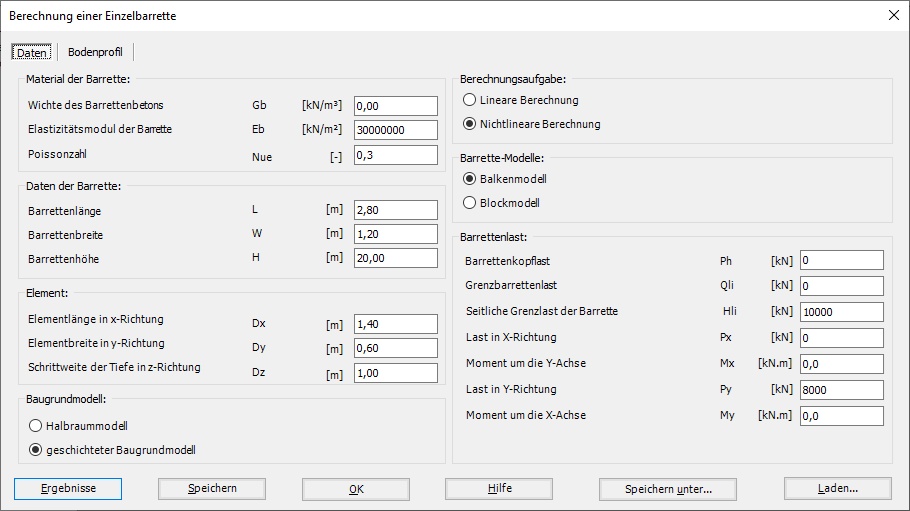
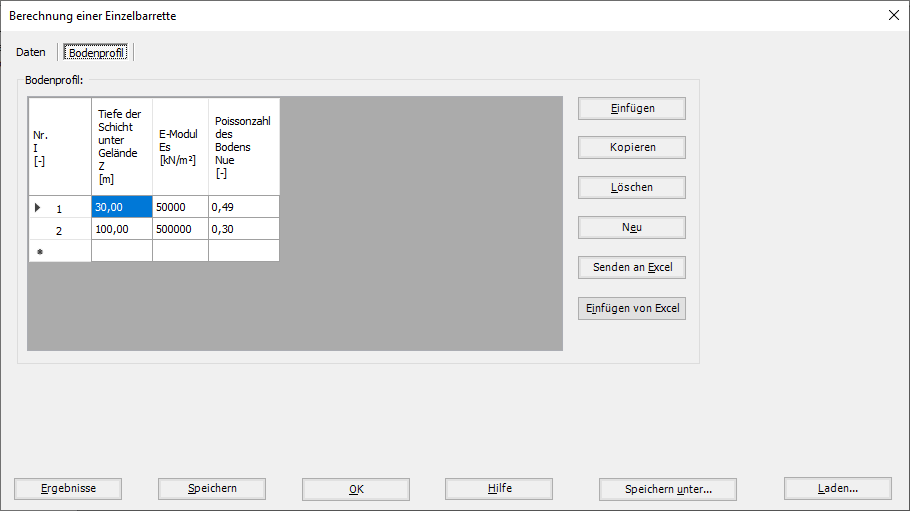
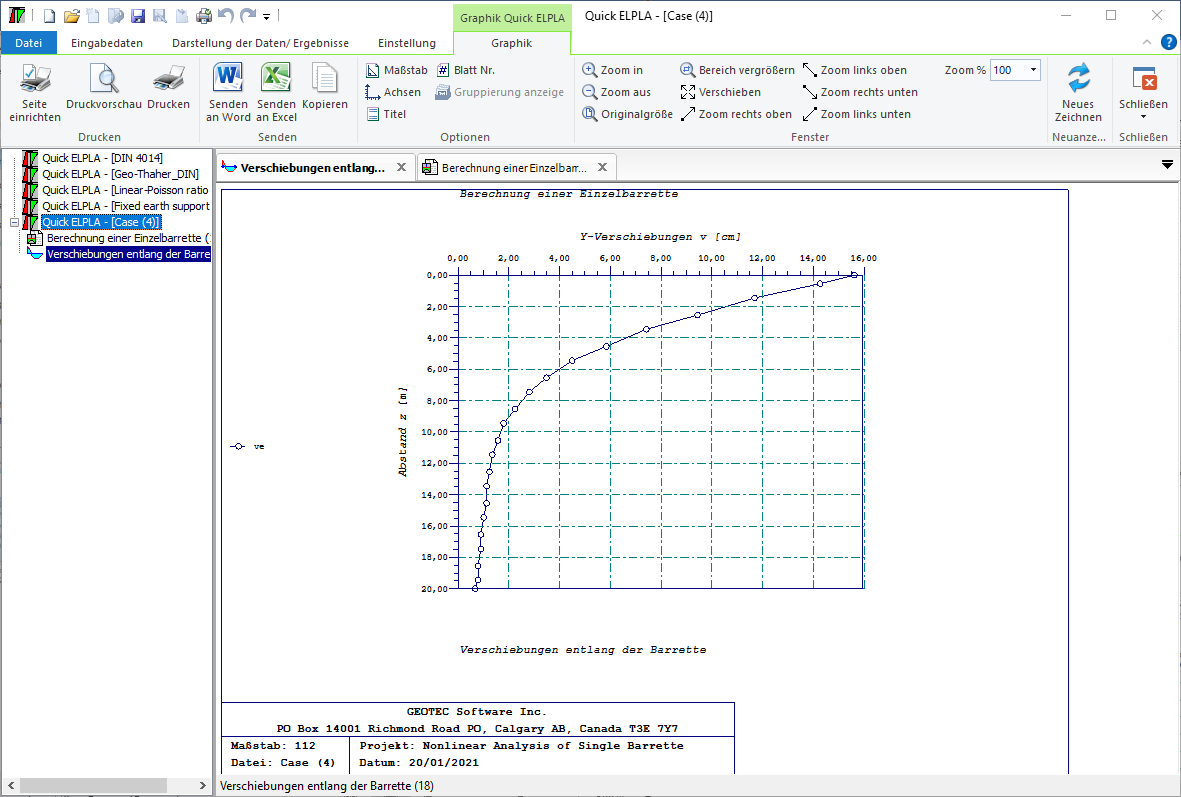
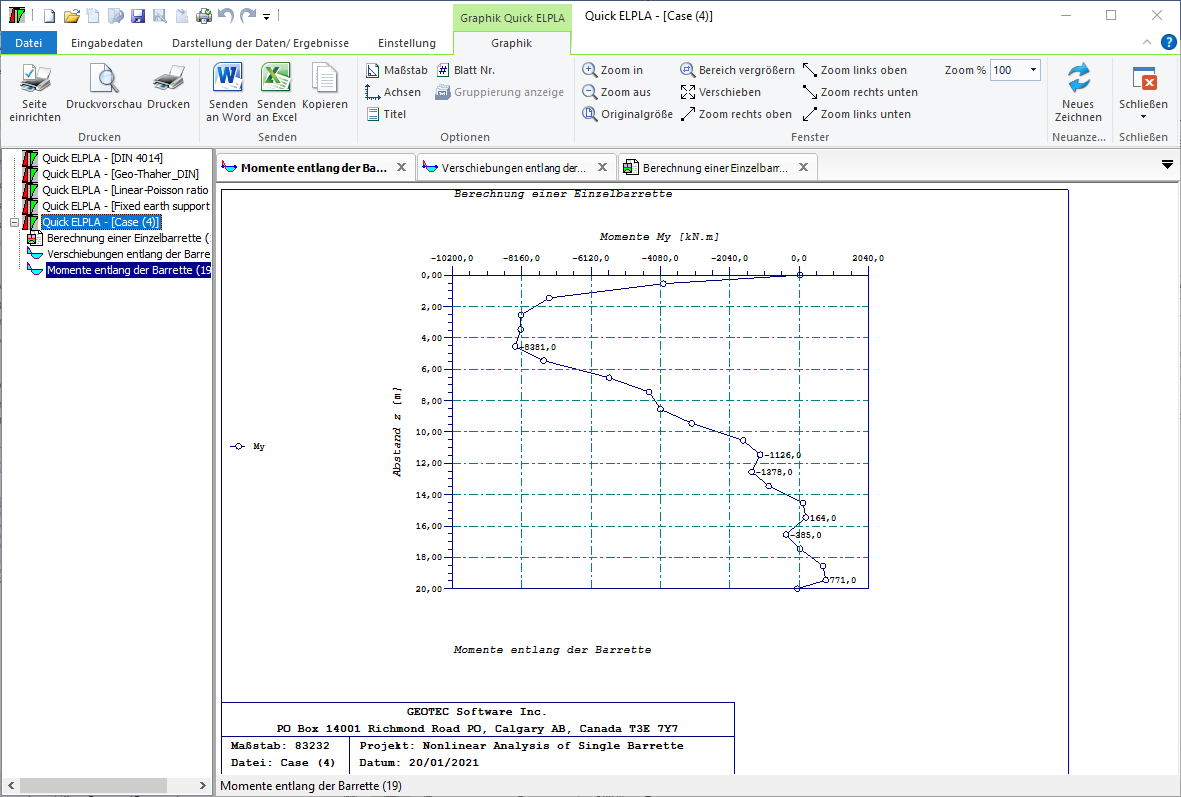
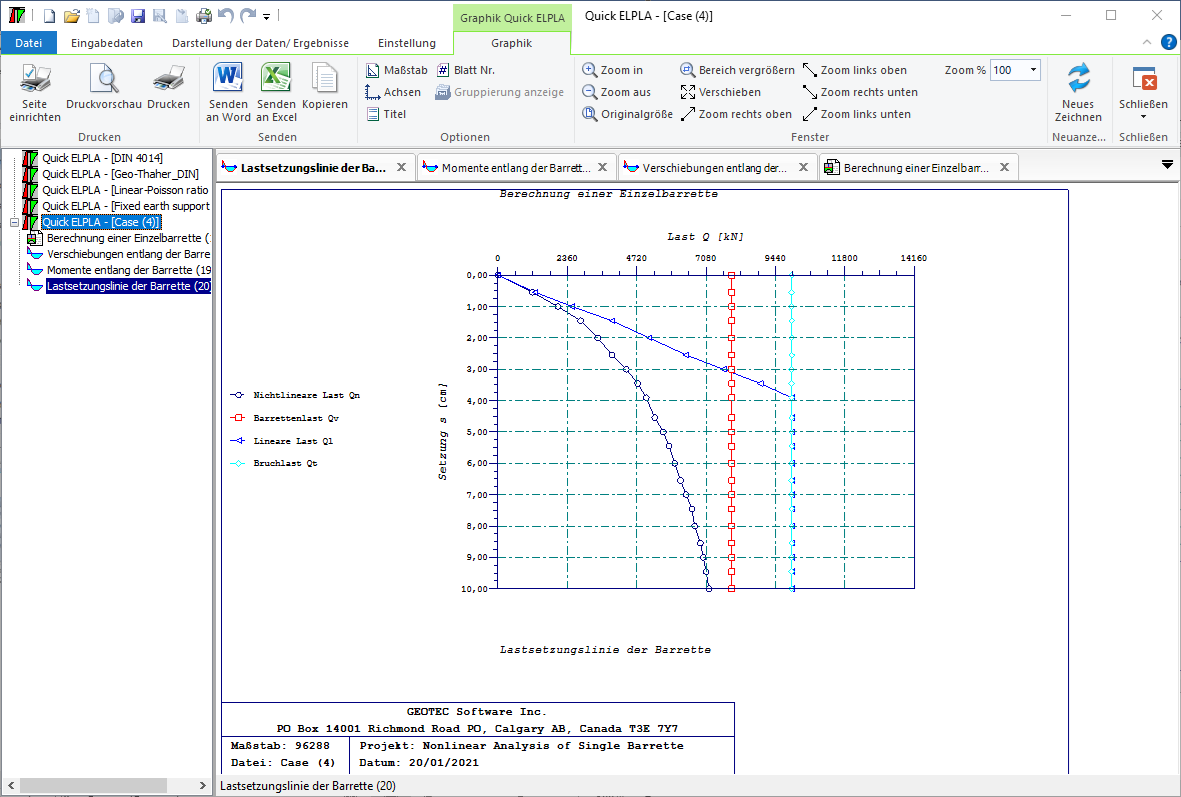
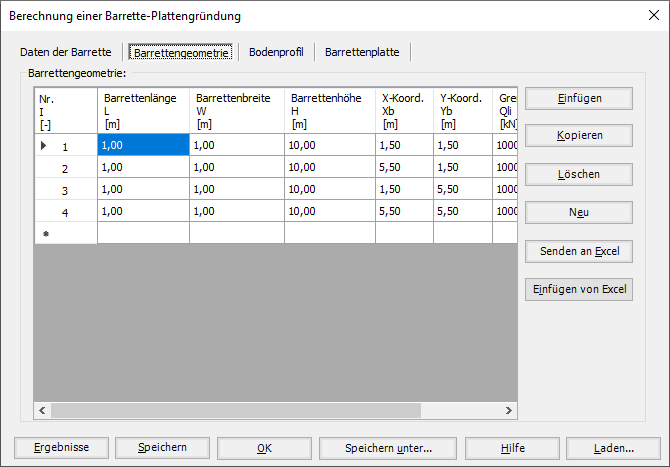
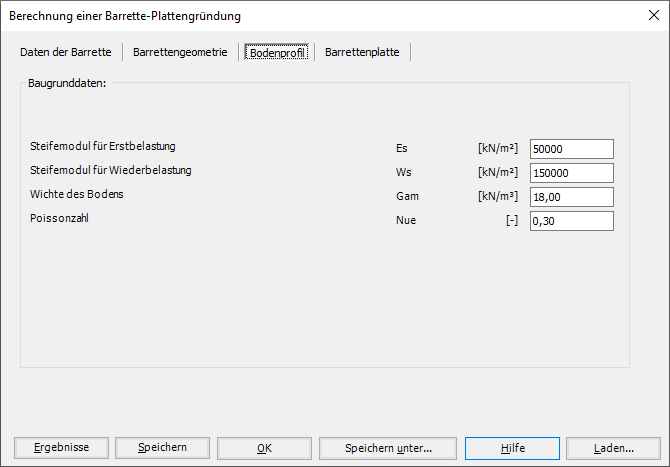
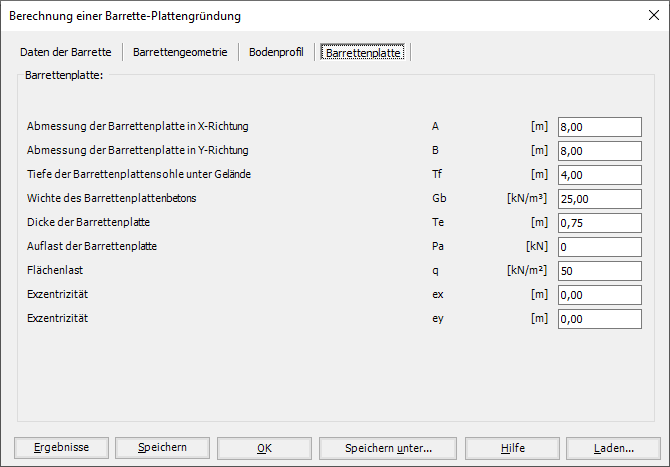
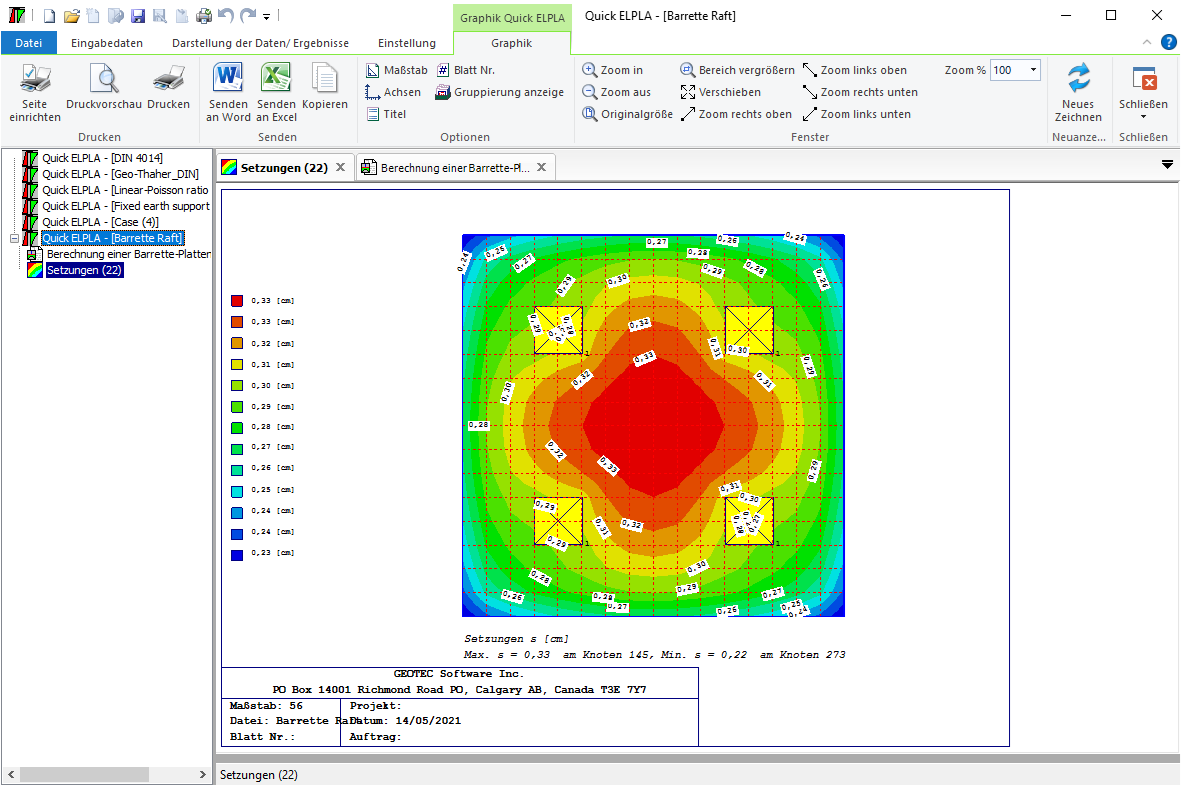
Die Berechnung von Barrettengruppen und Barrette-Plattengründung kann linear oder nichtlinear in folgenden Fällen durchgeführt werden:
- Elastische Barrettengruppen.
- Starre Barrettengruppen.
- Starre Barrette-Plattengründung.
- Elastische Barrette-Plattengründung.
Der seitliche Erddruck ist der Druck, den der Boden in horizontaler Richtung ausübt. Der seitliche aktive Erddruck am Punkt A im Boden ist gleich der effektiven Vertikalspannung σ'v multipliziert mit einem Koeffizienten, σh= ka σ'v. Wenn ein Grundwasserspiegel vorhanden ist, wird der horizontale hydrostatische Wasserdruck berücksichtigt. Der seitliche Wasserdruck am Punkt A im Boden ist das Gewicht der Wassersäule über diesem Punkt w=γwz.