The definition of the characteristic point so according to Graßhoff (1955) can be used to verify the mathematical model of ELPLA for flexible foundation and rigid raft. The characteristic point of a uniformly loaded area on the surface is defined as that point of a flexible settlement so is identical with the rigid displacement wo. For a rectangular area, the characteristic point takes the coordinates ac =0.87A and bc = 0.87B, where A and B are the area sides.
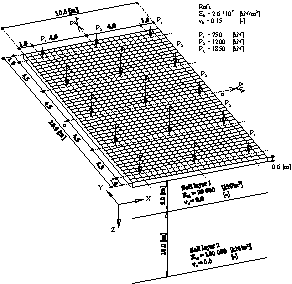
Figure 12 shows a raft of dimensions 8 [m] × 12 [m] resting on three different soil layers of thicknesses 7 [m], 5 [m] and 6 [m], respectively.
![]() Example 10: Flexible foundation and rigid raft on layered subsoil
Example 10: Flexible foundation and rigid raft on layered subsoil